
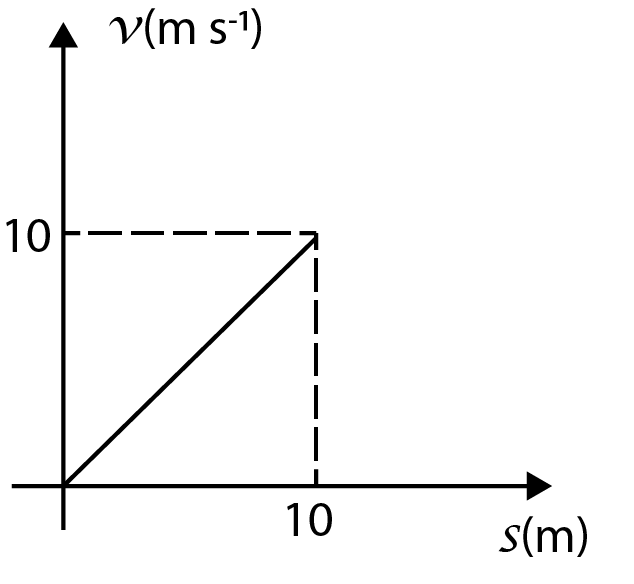
Velocity versus displacement graph of a particle moving in a straight line is shown in Fig. A.5. The corresponding acceleration versus velocity graph will be
A.
B.
C.

D.





Answer
451.2k+ views
Hint: To solve the question, you first need to find slope of the curve given in the question, and represent the slope as
Complete answer:
We will proceed with the solution exactly as explained in the hint section of the solution to the question.
As we can see in the given graph, the slope of the line can be given as:
If we substitute the value of coordinates of the two extreme points on the curve as
Now, we can see that
Let us write acceleration in terms of differentials:
If we multiply and divide the right-hand side of the equation by
We already know that velocity is given as:
So, the equation of acceleration becomes:
If we substitute the value of the term
After transposing, we get:
The curve for this equation will be nothing but a straight-line curve on which the value of acceleration is exactly the same as the value of velocity.
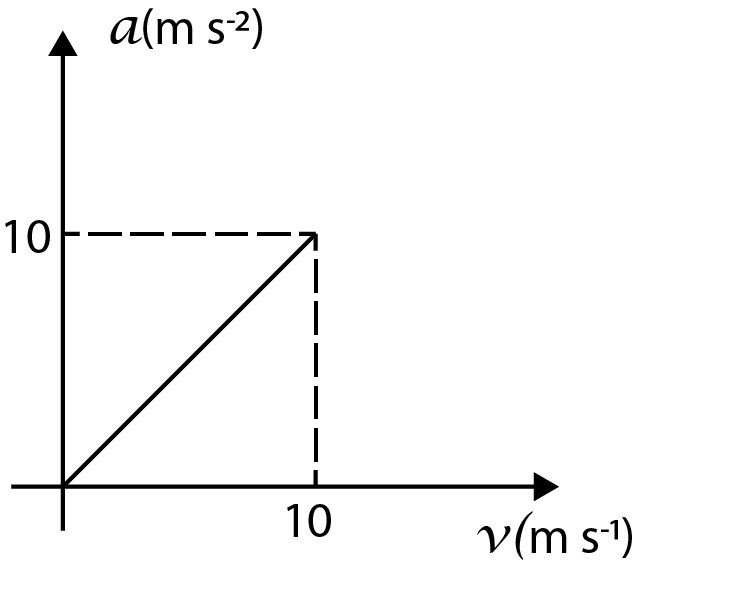
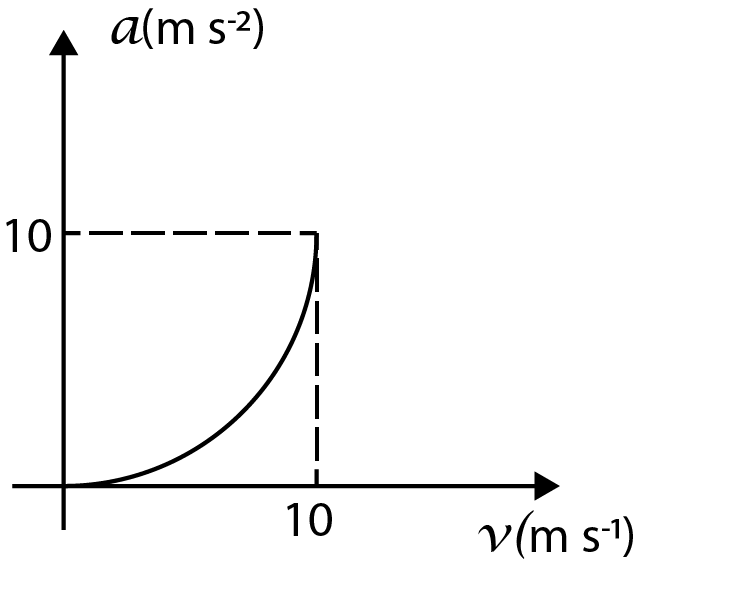
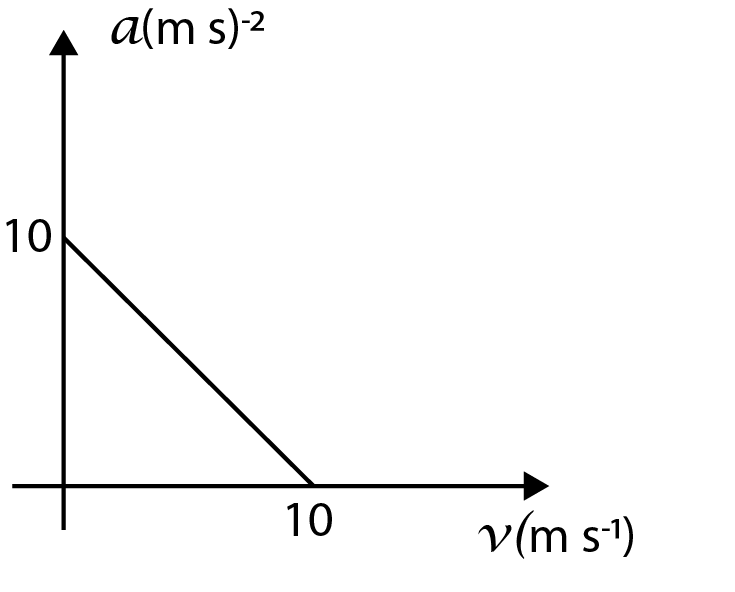
If we check the options, the only option whose curve matches with the curve that we described above is option (A).
Hence, the correct option is option (A).
Note:
The main confusion can be at the point that which straight-line curve is the correct one between option (A) and option (D). To solve this, we can clearly see in the curve given in the question that the initial value of velocity is zero, hence, the correct option will be the one where the straight line starts at origin and not from a constant value on the y-axis.
Complete answer:
We will proceed with the solution exactly as explained in the hint section of the solution to the question.
As we can see in the given graph, the slope of the line can be given as:
If we substitute the value of coordinates of the two extreme points on the curve as
Now, we can see that
Let us write acceleration in terms of differentials:
If we multiply and divide the right-hand side of the equation by
We already know that velocity is given as:
So, the equation of acceleration becomes:
If we substitute the value of the term
After transposing, we get:
The curve for this equation will be nothing but a straight-line curve on which the value of acceleration is exactly the same as the value of velocity.
If we check the options, the only option whose curve matches with the curve that we described above is option (A).
Hence, the correct option is option (A).
Note:
The main confusion can be at the point that which straight-line curve is the correct one between option (A) and option (D). To solve this, we can clearly see in the curve given in the question that the initial value of velocity is zero, hence, the correct option will be the one where the straight line starts at origin and not from a constant value on the y-axis.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




