Question

Volume of a spherical shell with outer and inner radii R and r respectively is:
A. $\dfrac{{4\pi }}{3}\left( {{R^3} - {r^3}} \right)$
B. $\dfrac{{4\pi }}{3}\left( {{R^3} + {r^3}} \right)$
C. $\dfrac{\pi }{3}\left( {{R^3} - {r^3}} \right)$
D. $\dfrac{\pi }{3}\left( {{R^3} + {r^3}} \right)$

Answer 1

Hint: Try to visualise two spheres having radii r and R by drawing a rough diagram and then by applying the formula of volume of a sphere, find the answer.

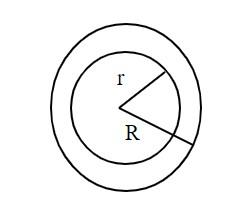
Complete Step-by-Step solution:
In this question, we are supposed to find the volume of the spherical shell, to do that first we are going to find the volume of the bigger sphere and then subtract the smaller sphere from it.
Let us take the radius of the bigger sphere as ‘R’ and the smaller sphere to be ‘r’.
Now to find the volume of the sphere we have a formula, so let us apply that,
Therefore,
Volume of bigger sphere=$\dfrac{{4\pi }}{3}{R^3}$
Similarly, we can find the volume of the smaller sphere,
Volume of the smaller sphere= $\dfrac{{4\pi }}{3}{r^3}$
To find the volume of the shell, we will subtract the volume of smaller sphere from the bigger sphere, therefore,
Volume of spherical shell=Volume of bigger sphere-Volume of smaller sphere
Volume of spherical shell=$\dfrac{{4\pi }}{3}{R^3}$-$\dfrac{{4\pi }}{3}{r^3}$
We can take $\dfrac{{4\pi }}{3}$ common, so that it becomes,
Volume of spherical shell= $\dfrac{{4\pi }}{3}\left( {{R^3} - {r^3}} \right)$
So, Option A is correct.

Note: Make sure while calculating the volume you do not convert the values in decimal and let it stay as fraction because if you observe the options given to us in question, they are in the form of fractions itself.