Question

What is the volume of the trapezoidal prism?

Answer 1

Hint: As in the given problem we are required to find the volume of a trapezoidal prism, we must first get to know what really a trapezoidal prism is. Upon doing that we will solve the problem in two steps, first we will find the area of the trapezoid i.e., the cross section of the said prism then as the second step we will directly multiply the length of the prism to the obtained area of the trapezoid. This will give us the volume of the assumed trapezoidal prism.

Complete step-by-step solution:
In the problem we have to find the volume of a trapezoidal prism.
Let’s first understand about trapezoidal prism. A trapezoidal prism is a solid shape in three-dimensional space that has two congruent trapezoids as its top and lower base. The rest surfaces are rectangles which are known as lateral faces of the prism. A trapezoid is basically a four-sided flat shape where the opposite sides parallel.

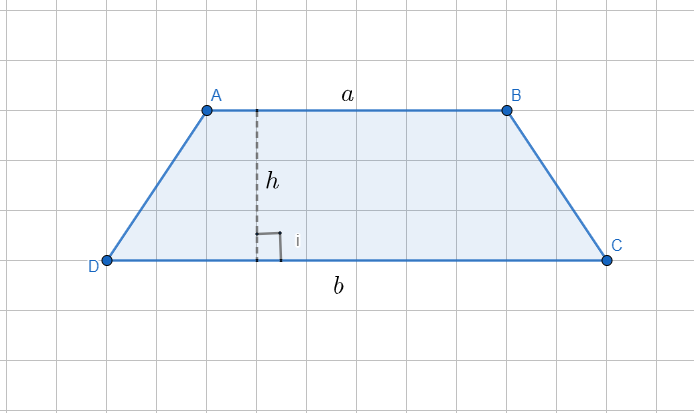
In the above picture we can see that the base of the trapezoid has a length of $b$ , the side parallel to the base has a length of $a$ and the height of the trapezoid is $h$ .
Now, we know that the formula of the area of a trapezoid is
\[Area=\dfrac{1}{2}\left( a+b \right)h\]
We assume that the length of the prism is \[l\] . So, if we multiply the area of the trapezoid to the length of the prism, we can get the volume of the trapezoidal prism.
Hence, $Volume=\dfrac{1}{2}\left( a+b \right)h\times l$
$\Rightarrow Volume=\dfrac{\left( a+b \right)hl}{2}$
Therefore, the volume of a trapezoidal prism is $\dfrac{\left( a+b \right)hl}{2}$ .

Note: While finding the area and volume of the prism we must keep in mind that the formula is applied properly and without any flaws so that mistakes are avoided. Also, we have to be careful while finding the area as different shapes have different formulas for finding their area.