Question

Water is dripping out from a conical funnel of semi-vertical angle \[\dfrac{\pi }{4}\]at the uniform rate of 2 \[c{{m}^{2}}/\sec \] in the surface through a tiny hole at the vertex of the bottom. When the slant height of the water level is 4cm, find the rate of decrease of the slant height of the water.

Answer 1

Hint: Consider the radius and height of the cone as ‘r’ and ‘h’. We have been given \[\dfrac{dA}{dt}\]. By using formula \[{{l}^{2}}={{r}^{2}}+{{h}^{2}}\], differentiate them w.r.t ‘t’. Differentiate, \[A=\pi {{r}^{2}}\], for the base of the cone and find \[\dfrac{dr}{dt}\]. Consider, \[\Delta ABC\], take \[\tan \theta \] and get values of r and h. Substitute all and get the value of \[\dfrac{dl}{dt}\].

Complete step-by-step answer:
Consider the figure drawn. It represents a conical funnel. The semi-vertical angle is \[\dfrac{\pi }{4}=\theta \].

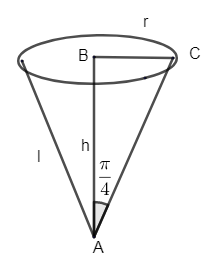
Let ‘r’ be the radius of the base of the conical funnel, h is the height and l is the slant height of the conical funnel. Here, l = 4cm.
Let ‘s’ be the surface area of the conical funnel.
From the question, it's given that the water is dripping at a uniform rate of 2 \[c{{m}^{2}}/\sec \].
\[\therefore \dfrac{dA}{dt}=-2c{{m}^{2}}/\sec -(1)\]
It is taken -2 \[c{{m}^{2}}/\sec \] because the area is decreasing.
i.e. we need to find \[\dfrac{dl}{dt}\].
At any time radius ‘r’, height ‘h’ and slant height ‘l’, gives
\[{{l}^{2}}={{r}^{2}}+{{h}^{2}}-(2)\]
Differentiating the above equation (2)
\[2l.\dfrac{dl}{dt}=2r.\dfrac{dr}{dt}+2h.\dfrac{dh}{dt}\]
Cancel out like terms.
\[\Rightarrow l.\dfrac{dl}{dt}=r.\dfrac{dr}{dt}+h.\dfrac{dh}{dt}-(3)\]
From equation (1) \[\dfrac{dA}{dt}=-2\]
We know \[A=\pi {{r}^{2}}\]
\[\begin{align}
  & \dfrac{d}{dt}\left( \pi {{r}^{2}} \right)=-2 \\
 & \Rightarrow 2\pi r.\dfrac{dr}{dt}=-2 \\
 & \therefore r.\dfrac{dr}{dt}=\dfrac{-2}{2\pi }=-\dfrac{1}{\pi }-(i) \\
\end{align}\]
From the figure consider \[\vartriangle ABC\]
By basic trigonometry,
\[\tan \theta =\]opposite side/ adjacent side\[=\dfrac{r}{h}\]
\[\theta =\dfrac{\pi }{4}\]and \[\tan \dfrac{\pi }{4}=1\]
\[\Rightarrow \dfrac{r}{h}=1\Rightarrow r=h\]
Now, differentiating r = h, in terms of ‘t’ we get,
\[\dfrac{dr}{dt}=\dfrac{dh}{dt}-(ii)\]
Similarly, from \[\vartriangle ABC\], taking the value of \[\sin \dfrac{\pi }{4}\]
\[\sin \dfrac{\pi }{4}=\]opposite side/Hypotenuse = \[\dfrac{r}{l}\]
We know, \[\sin \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}\]
\[\Rightarrow \dfrac{1}{\sqrt{2}}=\dfrac{r}{l}\], where l = 4
\[\begin{align}
  & \Rightarrow \dfrac{1}{\sqrt{2}}=\dfrac{r}{4}\Rightarrow r=\dfrac{4}{\sqrt{2}}=2\sqrt{2} \\
 & \therefore r=2\sqrt{2}-(iii) \\
\end{align}\]
\[h=2\sqrt{2}\] and \[l=4\]
Now consider the equation (3), substitute the values of (i), (ii) and (iii)
$
\Rightarrow { l \dfrac{dl}{dt}=r\dfrac{dr}{dt}+h\dfrac{dh}{dt}}$
$\Rightarrow {4\dfrac{dl}{dt}=2\sqrt{2}\dfrac{dr}{dt}+2\sqrt{2}\dfrac{dr}{dt}}$
$\Rightarrow {4\dfrac{dl}{dt}=4\sqrt{2}\dfrac{dr}{dt}}$
$\Rightarrow {\because \dfrac{dr}{dt}=\dfrac{dh}{dt}}$
$\Rightarrow {r=h=2\sqrt{2},l=4}$

From (i) we got
\[\begin{align}
  & r.\dfrac{dr}{dt}=\dfrac{-1}{\pi } \\
 & \Rightarrow \dfrac{dr}{dt}=\dfrac{-1}{\pi .r}=\dfrac{-1}{2\sqrt{2}.\pi } \\
\end{align}\]
\[\therefore 4\dfrac{dl}{dt}=\dfrac{-4\sqrt{2}}{2\sqrt{2}\pi }\]
\[\dfrac{dl}{dt}=\dfrac{-2}{4\pi }=\dfrac{-1}{2\pi }\]

\[\therefore \dfrac{dl}{dt}=\dfrac{-1}{2\pi }\]
\[\therefore \]Rate of decrease of slant height of water is \[\left( \dfrac{1}{2\pi } \right)\].

Note: We need to find the rate of decrease of slant height of water so take the uniform rate of flow as - 2 \[c{{m}^{2}}/\sec \]. If It was to find the rate of increase of slant height, then take it as 2 \[c{{m}^{2}}/\sec \]. Students should remember the formula of surface area of cone and relationship between radius,height and slant height of cone i.e \[{{l}^{2}}={{r}^{2}}+{{h}^{2}}\] for solving these types of questions.