Question

Water is flowing at the rate of 5km per hour through a pipe of diameter 14cm into a rectangle tank, which is 50m long and 44m wide. Find the time in which the level of water in the tank will rise by 7cm.
$
  {\text{A}}{\text{. 2hr}} \\
  {\text{B}}{\text{. 3hr}} \\
  {\text{C}}{\text{. 4hr}} \\
  {\text{D}}{\text{. 1hr}} \\
$

Answer 1

Hint: In this question we will equate the volume of water flowed from the pipe and the volume of the tank that needs to be filled. This will help us simplify the question and reach the answer.

Complete step-by-step answer:

We have been given that the water is flowing at the rate of 5km per hour through a pipe of diameter 14cm.

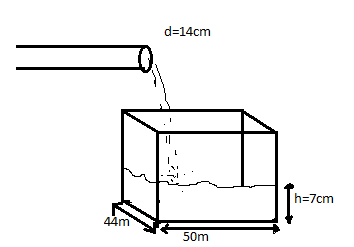
So the volume of water flowing through the pipe $ = {\text{Rate of flow of Water }} \times {\text{ time }} \times {\text{ Area of pipe}}$
Now, let the time taken be t
So, the volume of water flowing through the pipe
 $ = 5000m/hr \times t{\text{ }}hr \times \pi {\left( {0.07m} \right)^2}$
$ = 77t{\text{ }}{{\text{m}}^3}$
And the volume of water to be filled in the tank
$ = {\text{ Length}} \times {\text{Width}} \times {\text{Height}}$
$ = 50m \times 44m \times 0.07m$
$ = 154 m^3$
Now the volume of water flowing from the pipe is equal to the volume of the tank that needs to be filled.
So, 77t = 154
Therefore, t = 2 hr
Hence, it takes 2 hours for the level of water to rise by 7cm.
So, the option A is correct.

Note: Whenever we face such types of problems the main point to remember is that we need to have a good grasp over mensuration and its formulas. In these types of questions, we should always find both the volumes separately and then proceed. This helps in getting us the required condition and gets us on the right track to reach the answer.