Question

Water is leaking from a conical funnel at the rate of \[5c{m^3}/\sec \]. If the radius of the base of the funnel is 10 cm and the altitude is 20 cm. Find the rate at which the water level is dropping when it is 10 cm from the top.

Answer 1

Hint: In this question remember the method of differentiation also remember to use ratio of radius and height to put in the formula of conical flask i.e. $V = \dfrac{1}{3}\pi {r^2}h$, using this information will help you to approach closer towards the solution of the question.

Complete step-by-step solution:

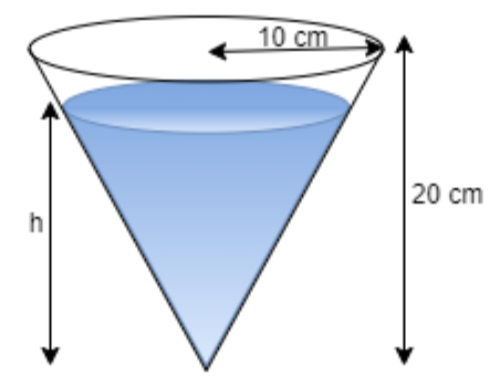
According to the given information we have a conical funnel leaking water at the rate of \[5c{m^3}/\sec \] which means that decrease in volume is \[5c{m^3}/\sec \] i.e. \[\dfrac{{dv}}{{dt}} = 5c{m^3}/\sec \]
The radius of conical funnel is 10 cm i.e. r = 10 cm and altitude is 20 cm i.e. h = 20 cm
We know that the volume of the conical flask is given by $V = \dfrac{1}{3}\pi {r^2}h$ here r is the radius base of conical flask and h is the height of conical flask
Let $V = \dfrac{1}{3}\pi {r^2}h$ take this formula as equation 1
As we know that the ratio of radius and height of conical flask will remain same when the flask is full of water
So, $\dfrac{r}{h} = \dfrac{{10}}{{20}}$
$ \Rightarrow $$\dfrac{r}{h} = \dfrac{1}{2}$
$ \Rightarrow $$r = \dfrac{h}{2}$
Substituting the given values in the equation 1 we get
$V = \dfrac{1}{3}\pi {\left( {\dfrac{h}{2}} \right)^2}h$
$ \Rightarrow $$V = \dfrac{1}{3} \times \pi \times \dfrac{{{h^3}}}{4}$
$ \Rightarrow $$V = \dfrac{1}{{12}} \times \pi \times {h^3}$
Differentiating the above equation both side with respect to t we get
$\dfrac{{dV}}{{dt}} = \dfrac{1}{{12}} \times \pi \times 3{h^2} \times \dfrac{{dh}}{{dt}}$
Substituting the values in the above equation we get
$5 = \dfrac{1}{4} \times \pi \times {\left( {10} \right)^2} \times \dfrac{{dh}}{{dt}}$
$ \Rightarrow $$\dfrac{{dh}}{{dt}} = \dfrac{{5 \times 4}}{{100 \times \pi }}$
$ \Rightarrow $\[\dfrac{{dh}}{{dt}} = \dfrac{{20 \times 7}}{{100 \times 22}}\]= $0.0\overline {63} $ cm/sec
Therefore the rate of water level dropping in conical flask when water starts leaking is $\dfrac{{dh}}{{dt}}$ = 0.063 cm/sec.

Note: In the above solution we used the method of differentiation which can be defined as the method to calculate the change in rate of some quantity with respect to another let take the help of an example to explain this concept suppose a driver is driving his car with speed of 12 km/hr having acceleration of $3\dfrac{m}{{sec}^{2}}$ so here acceleration is the rate of change in speed of car with respect to time that means in every second the speed of car will increase by $3\dfrac{m}{{sec}^{2}}$ so as shown in example the method of differentiation helps to find the rate of change in quantity with respect to time or other quantity.