
We know that
Answer
503.7k+ views
Hint: To solve the above question, you need to individually solve the right-hand side and left-hand side of the equation individually by putting the required values and show that both sides of the equation are equal. For putting the required values you need to use the trigonometric ratio table contains the values of different trigonometric ratios for trigonometric standard angles such as
Complete step by step solution:
Before moving to the solution, let us discuss the nature of sine and cosine function, which we would be using in the solution. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.
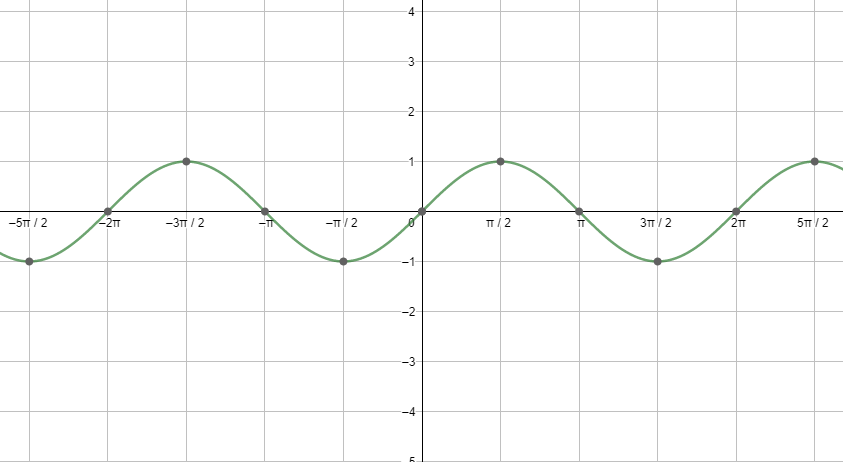
Next, let us see the graph of cosx.
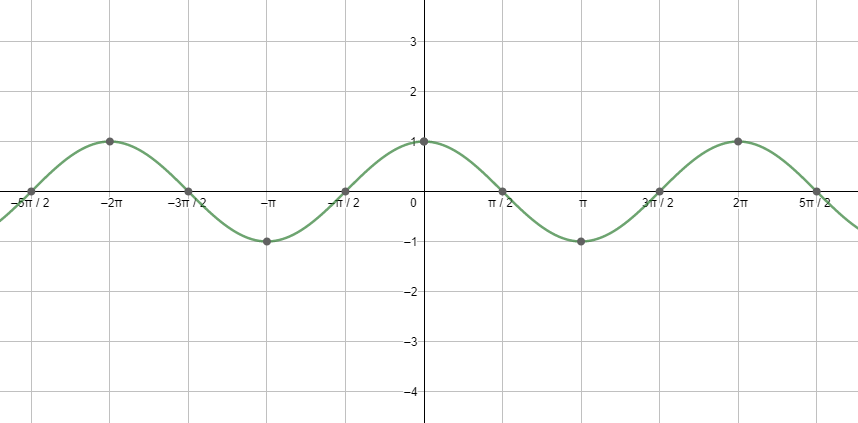
Looking at both the graphs, and using the relations between the different trigonometric ratios, we get
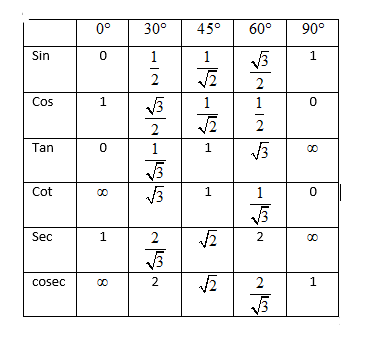
Let us start the solution to the above question by simplifying the left-hand side of the equation
And we know that the value of
So, the left-hand side of the equation
Now let us simplify the right-hand side of the equation by putting the values
Now we know that
Therefore, we can say that the left-hand side of the equation
Note: Be careful while putting the values of the different trigonometric ratios in the expression for solving the question. Also, be careful with the calculation part, as, in such questions, most errors occur in the calculation part. For example: students in a hurry write
Complete step by step solution:
Before moving to the solution, let us discuss the nature of sine and cosine function, which we would be using in the solution. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

Next, let us see the graph of cosx.

Looking at both the graphs, and using the relations between the different trigonometric ratios, we get

Let us start the solution to the above question by simplifying the left-hand side of the equation
And we know that the value of
So, the left-hand side of the equation
Now let us simplify the right-hand side of the equation by putting the values
Now we know that
Therefore, we can say that the left-hand side of the equation
Note: Be careful while putting the values of the different trigonometric ratios in the expression for solving the question. Also, be careful with the calculation part, as, in such questions, most errors occur in the calculation part. For example: students in a hurry write
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




