Question

What are coincident lines?

Answer 1

Hint: We can compare lines with each other. We know that the parallel lines are defined with respect to a line as well as the perpendicular lines. Similarly, coincident lines are also defined on the basis of a fixed line.

Complete step by step solution:
We know that two lines are called coincident lines when they coincide with each other or when they lie on top of each other.
We can say that we can call more than two lines coincident if they are all lying on top of each other.
Suppose we have a straight line $L$ in the $xy-$plane joining the points $\left( a,b \right)$ and $\left( p,q \right).$ If there exists another straight line $M$ in the $xy-$plane joining the same points $\left( a,b \right)$ and $\left( p,q \right),$ we say that the lines $L$ and $M$ are coincident lines.
Given below is the graphical representation of the coincident lines $L$ and $M.$

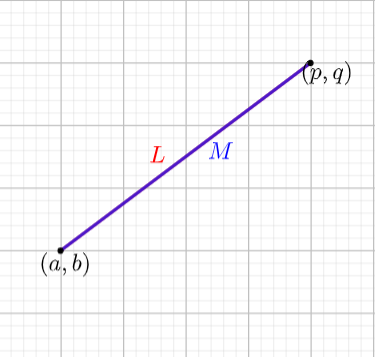
We cannot see these two lines separately.
Let us suppose that there are the straight lines $N,O,P,Q$ in the same plane joining the same points as $L$ and $M.$ We say that these lines are all coincident with $L$ and $M.$
Now, let us consider the equations of straight lines. Suppose that we have a line $x+y=4,$ then the line$3x+3y=12$ is a coinciding line. We can see that the second line is thrice the first line.
We are comparing the positions of the lines. If the positions are the same, if all the points through which these lines are passing are the same, then the lines are coinciding lines.
We can define an equivalent relation as follows: the line ${{l}_{1}}$ is related to the line ${{l}_{2}},$ if ${{l}_{1}}$ and ${{l}_{2}}$ are coincident lines.
Since the line ${{l}_{1}}$ lies in the same position as ${{l}_{1}},$ we can say ${{l}_{1}}$ is coincident to itself. And so, we can say that ${{l}_{1}}$ is coincident with ${{l}_{1}}$ which implies that ${{l}_{1}}$ is related to itself. Therefore, this relation is reflexive.
Suppose that the line ${{l}_{1}}$ is related to the line ${{l}_{2}}.$ That means, ${{l}_{1}}$ and ${{l}_{2}}$ are coincident lines. We can say that ${{l}_{2}}$ and ${{l}_{1}}$ are coincident lines. This implies that ${{l}_{2}}$ is related to ${{l}_{1}}.$ Therefore, this relation is symmetric.
Let us suppose that ${{l}_{1}}$ is related to ${{l}_{2}}$ and ${{l}_{2}}$ is related to ${{l}_{3}}.$ Then, ${{l}_{1}}$ and ${{l}_{2}}$ are coincident lines and ${{l}_{2}}$ and ${{l}_{3}}$ are coincident lines. We can say that these three lines are coincident lines. So, we can say that ${{l}_{1}}$ and ${{l}_{3}}$ are coincident lines. This implies that ${{l}_{1}}$ is related to ${{l}_{3}}.$ Therefore, this relation is transitive.
Hence this relation is an equivalence relation.

Note: We know that the relation of parallel lines is also an equivalent relation. But the relation of perpendicular lines is not an equivalence relation. Because it does not hold the transitivity property.