Question

What are coterminal angles?

Answer 1

Hint: In this type of question we consider the type of angle which depends on the standard position that means angles with the initial side on the positive x-axis. Also as we are considering the term with reference to angles obviously more than one angle exists here which we can obtain by adding or subtracting multiples of \[{{360}^{\circ }}\].

Complete step-by-step answer:
Now, we have to explain coterminal angles.
We can define coterminal angles as the angles who share the same initial side and terminal sides. In other words two angles are said to be coterminal if they are drawn in the standard position (angles with the initial side on the positive x-axis) and both will have their terminal sides in the same location.
We can also define coterminal angles as coterminal angles are two angles in the standard position and one angle is a multiple of \[{{360}^{\circ }}\] larger or smaller than the other.
In general, if \[\theta \] is any angle then \[\theta \pm n\left( {{360}^{\circ }} \right)\] is coterminal angle with \[\theta \] for all non-zero integer \[n\].
For example:

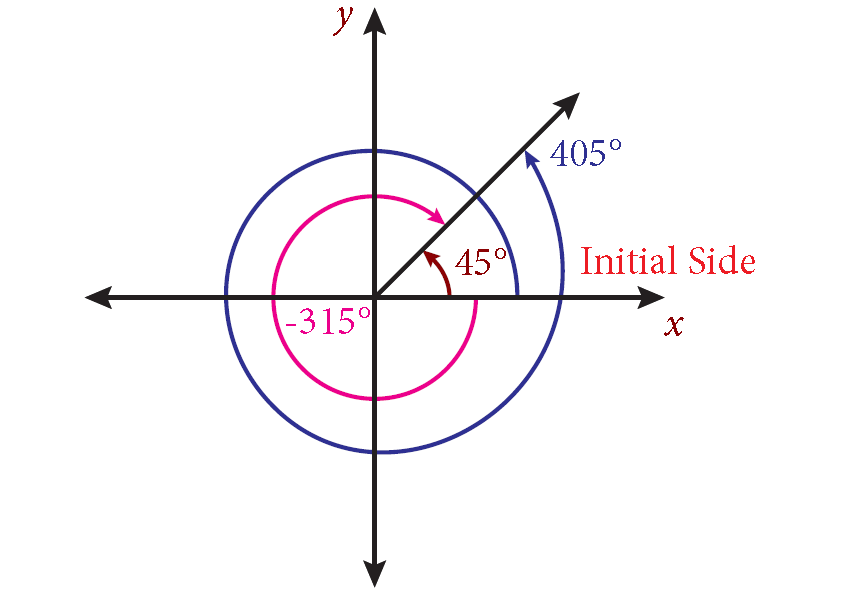
Here, we consider an angle of \[{{45}^{\circ }}\] so the corresponding coterminal angles are given by,
\[\Rightarrow {{45}^{\circ }}+{{360}^{\circ }}={{405}^{\circ }}\text{ and }{{45}^{\circ }}-{{360}^{\circ }}={{315}^{\circ }}\]


Note: In this question students have to note that if the angles are coterminal then both their terminal sides lie on top of each other. Also students have to note that if the angles are same then they are obviously coterminal but the angles can have different measures and still be coterminal. Also we have to note that for any angle there are infinite numbers of coterminal angles.