
What does
Answer
443.1k+ views
Hint: To solve the question, the concept of trigonometric value should be known. The values of trigonometric values for certain numbers should be known. Details of the trigonometric function is required to solve the question.
Complete step by step answer:
To start with some details on the trigonometric function,
On applying the same formula to find value of the given question,
With the help of the graph of
On applying the fact in equation (i), we get
This is undefined,
Note: Calculation of the trigonometric function with a certain angle becomes much easier with the help of the graph. Minimum and maximum value of the function could easily be known to us with the help of graphs. This is the graph of
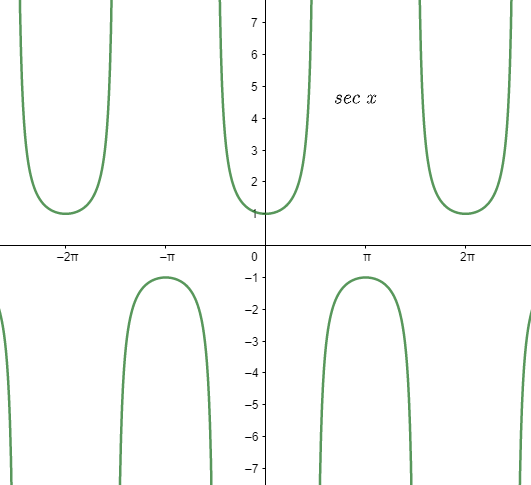
Now, let us see the graph of
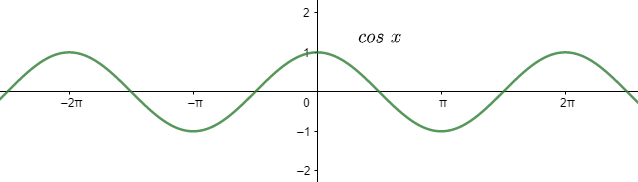
On differentiating both the graph we can at least infer that the trigonometric function
In this question the angle is in radian but sometimes the angle given is in the form of degree too , so we should know to convert the angle in radian to degree. So we can convert the unit of the angle as
Complete step by step answer:
To start with some details on the trigonometric function,
On applying the same formula to find value of the given question,
With the help of the graph of
On applying the fact in equation (i), we get
This is undefined,
Note: Calculation of the trigonometric function with a certain angle becomes much easier with the help of the graph. Minimum and maximum value of the function could easily be known to us with the help of graphs. This is the graph of

Now, let us see the graph of

On differentiating both the graph we can at least infer that the trigonometric function
In this question the angle is in radian but sometimes the angle given is in the form of degree too , so we should know to convert the angle in radian to degree. So we can convert the unit of the angle as
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




