Question

What is ‘a’ in a hyperbola?

Answer 1

Hint: We first explain the conic sections. Then we explain the special case of hyperbola and explain different parts of the conic.

Complete step-by-step solution:
In analytic geometry a hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. This intersection produces two separate unbounded curves that are mirror images of each other.
every hyperbola has two axes of symmetry. The transverse axis is a line segment that passes through the centre of the hyperbola and has vertices as its endpoints. The foci lie on the line that contains the transverse axis. The conjugate axis is perpendicular to the transverse axis and has the co-vertices as its endpoints. The centre of a hyperbola is the midpoint of both the transverse and conjugate axes, where they intersect. Every hyperbola also has two asymptotes that pass through its centre. As a hyperbola recedes from the centre, its branches approach these asymptotes. The central rectangle of the hyperbola is centered at the origin with sides that pass through each vertex and co-vertex; it is a useful tool for graphing the hyperbola and its asymptotes.
For the conic sections like hyperbola, general formula is \[\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1\].
Here ‘a’ represents the distance b/w the center and vertex of the hyperbola.

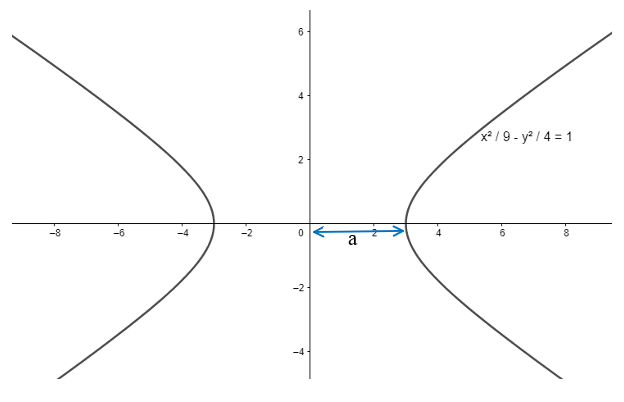
Note: In case of hyperbola the value of the eccentricity, the ratio of the distance from the focus to the horizontal distance from the directrix is greater than 1. We denote it with $e$ where $e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}$.