Question

What is a modified box plot?

Answer 1

Hint: Modified boxplot will show the outliers. Here, we will extend the lines to the highest and lowest values that are not the outliers. We will then mark the outliers separately. Outliers are the values that are far outside the pattern established by the rest of the data. They are very high or very low values in comparison to the rest of the data set.

Complete step-by-step answer:
Let us first see what a box is. Box plot is a way to abstract a set of data that is estimated using an interval scale. In this plot, all the data from multiple sources are summarized and displayed in a single graph. We can use this plot when we are given with multiple datasets from various sources which are related to each other. For example, we can use this plot if we have annual scores of various classes.
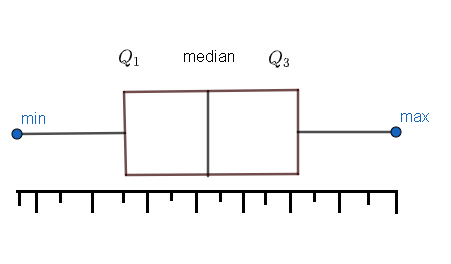
Now, we have to know box plot deeply to move onto its modified version. So, first we have to see how a box plot is drawn. The box plot will have five-number summary of a set of data. We can list these five-number as follows.
(i) The minimum value in the dataset. We have to display this number at the far left end.
(ii) The first quartile $\left( {{Q}_{1}} \right)$ . This will be placed at the left side in between the minimum value and median. ${{Q}_{1}}$ will be a value below the lower 25% of data contained.
(iii) The median value. We will represent this by a line that will be drawn at the centre of the box.
(iv) The third quartile $\left( {{Q}_{3}} \right)$ . This quartile will be at the right side in between the median and the maximum value. ${{Q}_{3}}$ will be a value above the lower 25% of data contained.
(v) The maximum value in the dataset which we will be representing at the far right end.
The box plot is shown below.

Now, we have to understand the concept of outliers. Outliers are the values that are far outside the pattern established by the rest of the data. They are very high or very low values in comparison to the rest of the data set. Let us consider the scores of a test $\left\{ 90,98,89,88,46,90,91,84,94 \right\}$
Here we can see that 46 is the outlier because it is a really low value when compared to the rest of the scores.
In a boxplot, we usually marks the maximum and minimum according to the values of the dataset. Let us draw a boxplot of $\left\{ 90,98,89,88,46,91,92,84,94 \right\}$ . We have to arrange the data in the increasing order. We will get $\left\{ 46,84,88,89,90,91,92,94,98 \right\}$ .
Now, we have to find the range by subtracting minimum value from the maximum value.
\[\begin{align}
  & \Rightarrow \text{Range }=\text{ Maximum value - Minimum value} \\
 & \Rightarrow \text{Range }=\text{ }98-46=52 \\
\end{align}\]
Now, we have to find the median which is the centre value of the given data.
$\Rightarrow \text{Median}=90$
Now, we have to find ${{Q}_{1}}$ . First quartile is the median of data values present at the left side of median. Therefore, we have to find the median of 46, 84, 88, 89.
$\begin{align}
  & \Rightarrow {{Q}_{1}}=\text{Median}\left( 46,84,88,89 \right) \\
 & \Rightarrow {{Q}_{1}}=\dfrac{84+88}{2}=\dfrac{172}{2}=86 \\
\end{align}$
Now, let us find ${{Q}_{3}}$ . First quartile is the median of data values present at the right side of median. Therefore, we have to find the median of 91, 92, 94, 98.
$\begin{align}
  & \Rightarrow {{Q}_{3}}=\text{Median}\left( 91,92,94,98 \right) \\
 & \Rightarrow {{Q}_{3}}=\dfrac{92+94}{2}=\dfrac{186}{2}=93 \\
\end{align}$
Now, we have to find the interquartile range by subtracting ${{Q}_{1}}$ from ${{Q}_{3}}$ .
\[\Rightarrow \text{Interquartile range}={{Q}_{3}}{{Q}_{1}}~=93-86=7\]
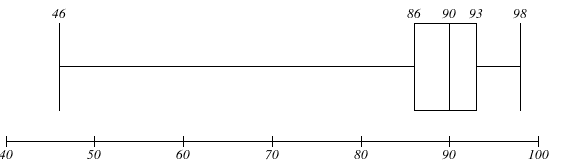
We know that the five-number summary is given by Minimum, ${{Q}_{1}}$ , Median, ${{Q}_{3}}$ , Maximum. That is, 46, 86, 90, 93, 98.
Hence, the box plot is drawn as follows.

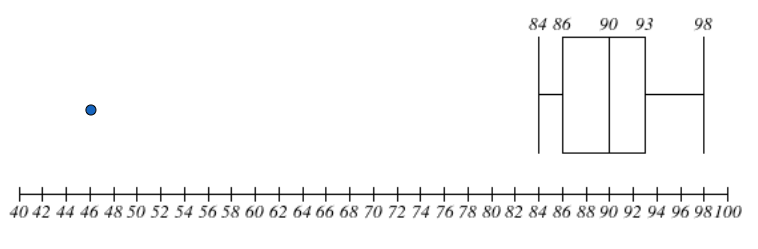
Now, we have to draw the modified boxplot. This boxplot will show the outliers. Here, we will extend the lines to the highest and lowest values that are not the outliers. We will then mark the outliers separately. In the dataset of test scores, we can see that the minimum value is 46 and 46 is the outliers. Hence, we have to look for the next minimum value. Here, this value will be 84. Hence, we will stretch the line to 84 and mark the outlier 46 separately (dot shown in the figure). The modified box plot will be as shown below.

Note: Some dataset contains more than one outliers or none. Students must know what outliers are to draw a modified boxplot. They must know how to find the five-summary numbers and how they are plotted.