Question

What is a polar equation?

Answer 1

Hint: Consider a point on the Cartesian plane as P(x, y). Now, define the radius vector by joining this point with the origin and consider it as $\overrightarrow{r}$ whose magnitude is r. Assume the angle this vector makes with the positive direction of x axis as $\theta $. Now, find the relation between the Cartesian coordinates x and y with r and $\theta $. Now, form a relation between r and $\theta $ to get the polar equation.

Complete step by step solution:
Here we have been asked about the term polar equation. Let us see its meaning and relation with Cartesian coordinates in a 2 – D plane.
Now, in mathematics the polar equation is the relation between the position vector of a point lying on a curve and the angle subtended by this vector with the positive direction of x axis. Let us assume a point P(x, y) lying in the Cartesian plane. Let us join the origin with the point P with a line whose direction is towards P and assume the angle subtended by the line with the positive direction of x axis is $\theta $.

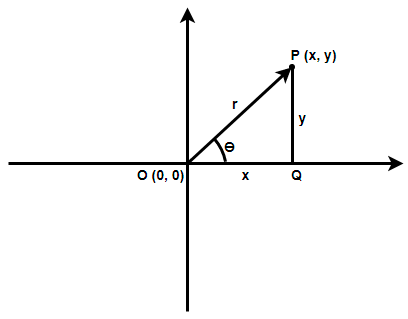
In the above figure we have a right angle triangle PQO with the side PQ as the perpendicular because it is opposite to the angle $\theta $. The side OQ is the base and OP is the hypotenuse. We have considered \[\overrightarrow{OP}\] as $\overrightarrow{r}$ which is known as the position vector of the point. The magnitude of this position vector is r. Now, in the right angle triangle PQO we have,
$\Rightarrow OP=r,OQ=x$ and $PQ=y$
Using the relation $\sin \theta =\dfrac{p}{h}$ and $\cos \theta =\dfrac{b}{h}$ where p = perpendicular, b = base and h = hypotenuse we get,
\[\begin{align}
  & \Rightarrow \sin \theta =\dfrac{y}{r} \\
 & \Rightarrow y=r\sin \theta ........\left( i \right) \\
\end{align}\]
\[\begin{align}
  & \Rightarrow \cos \theta =\dfrac{x}{r} \\
 & \Rightarrow x=r\cos \theta ........\left( ii \right) \\
\end{align}\]
Therefore, equation (i) and (ii) represents the relation between Cartesian coordinates (x, y) and polar coordinates $\left( r,\theta \right)$. So, if we are provided with any equation in Cartesian form then what we do is we replace x with $r\cos \theta $ and y with $r\sin \theta $ and simplify the relation. The equation obtained between r and $\theta $ will be called the polar equation.

Note: Note that if you will add the relations (i) and (ii) after squaring them then you will get the relation between the position vector and x and y coordinates which can be given as ${{r}^{2}}={{x}^{2}}+{{y}^{2}}$. This is a very important relation used in the chapter complex numbers to reduce the calculations. You may remember the polar equation of a circle given as $\left| r \right|=a\cos \theta $ or $\left| r \right|=a\sin \theta $.