Question

What is centripetal force?

Answer 1

Hint: In order to make a body move in a circular motion, we need a force called centripetal force. It is a force without which a body cannot move in a circular orbit. It depends on the mass, velocity of the object and radius of the circle in which it moves.

Detailed step by step solution:
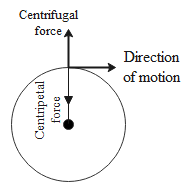
Centripetal force is the force required to make a body move in a curvilinear path. This is a force which can be observed both from the stationary frame and the frame of the reference of the rotating body.

The expression for centripetal force is given:

${F_C} = \dfrac{{m{{\text{v}}^2}}}{r}$

For a body which moves in a circular orbit, the translational velocity is given in terms of angular velocity by the following relation:

${\text{v}} = r\omega $

where $\omega $ is the angular velocity. Using this relation, we can get another expression for centripetal force given as

${F_C} = m{\omega ^2}r$

The direction of centripetal force is such that it is always directed towards the centre of rotation. It can be experienced as a force which tries to pull a rotating body towards the centre of rotation.

Examples:
1. Earth revolves around the sun due to the centripetal force provided by the gravitational force of attraction between earth and sun.
2. In a merry go round, the person experiences an inward force at every point of the motion.

Note: Centripetal force is different from centrifugal force in the sense that centrifugal force acts outwards while the centripetal force acts inwards. Centripetal force can be observed from both moving and stationary frames while centrifugal force can only be observed from the rotating frame of reference.