
What is tan cos and sin?
Answer
538.5k+ views
Hint: This question is from the trigonometry. We can say that the terms sin, cos, and tan are the trigonometric functions. We will understand this question is from a right angled triangle. We will understand what we call the sides of a right angled triangle. After that, from the right angled triangle we will understand and find the values of sin, cos and tan.
Complete step by step solution:
In this question, we are going to know about tan, cos and sin.
Let us take a right angled triangle.
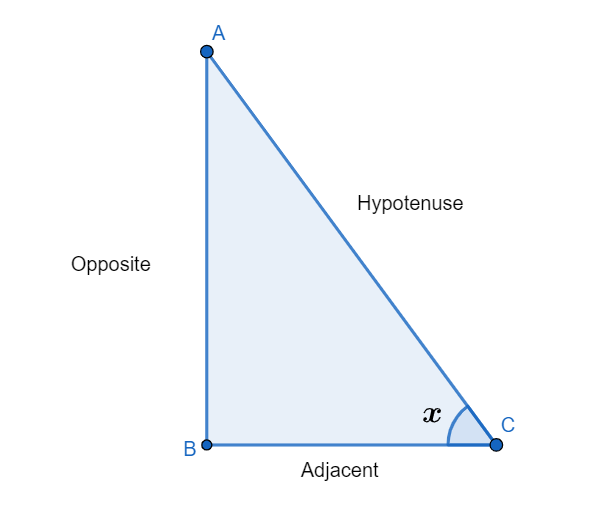
In the above figure, we can see that triangle ABC is a right angled triangle. In the above triangle, AC is hypotenuse or the longest side of the triangle, the side BC is adjacent to the angle \[x\], and the side AB is opposite to the angle \[x\].
Now, let us understand the values of sin, cos and tan from the above triangle.
If the angle is \[x\], then
\[\sin x=\dfrac{opposite}{hypotenuse}\]
\[\cos x=\dfrac{adjacent}{hypotenuse}\]
\[\tan x=\dfrac{opposite}{adjacent}\]
The term \[\tan x\] can also be written as the ratio of sin and cos that is \[\dfrac{\sin }{\cos }\].
For any angle, ratio stays the same no matter how big or small the triangle is.
Note: We should have a better knowledge in the topic of trigonometry. Always remember that the ‘sin’ term is the ratio of opposite and hypotenuse, the ‘cos’ term is the ratio of adjacent and hypotenuse, and the ‘tan’ term is the ratio of opposite and adjacent.
Always remember that the adjacent side is always next to the angle and the opposite side is always opposite of the given angle.
We can take reference from the following figure.
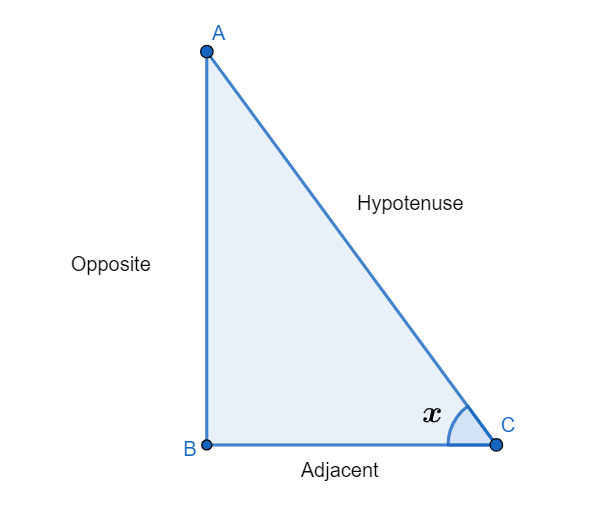
Complete step by step solution:
In this question, we are going to know about tan, cos and sin.
Let us take a right angled triangle.

In the above figure, we can see that triangle ABC is a right angled triangle. In the above triangle, AC is hypotenuse or the longest side of the triangle, the side BC is adjacent to the angle \[x\], and the side AB is opposite to the angle \[x\].
Now, let us understand the values of sin, cos and tan from the above triangle.
If the angle is \[x\], then
\[\sin x=\dfrac{opposite}{hypotenuse}\]
\[\cos x=\dfrac{adjacent}{hypotenuse}\]
\[\tan x=\dfrac{opposite}{adjacent}\]
The term \[\tan x\] can also be written as the ratio of sin and cos that is \[\dfrac{\sin }{\cos }\].
For any angle, ratio stays the same no matter how big or small the triangle is.
Note: We should have a better knowledge in the topic of trigonometry. Always remember that the ‘sin’ term is the ratio of opposite and hypotenuse, the ‘cos’ term is the ratio of adjacent and hypotenuse, and the ‘tan’ term is the ratio of opposite and adjacent.
Always remember that the adjacent side is always next to the angle and the opposite side is always opposite of the given angle.
We can take reference from the following figure.

Recently Updated Pages
An example of a disproportionation reaction is A 2KMnO4to class 10 chemistry CBSE

In an isosceles triangle ABC with AB AC D and E are class 10 maths CBSE

Area of triangle ABC whose sides are 24m 40m and 3-class-10-maths-CBSE

Find the sum of the first 50 even positive integer class 10 maths CBSE

The process by which plants lose water by evaporation class 10 biology CBSE

If the two circles touches externally then the distance class 10 maths CBSE

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the missing number in the sequence 259142027 class 10 maths CBSE




