Question

What is the bond order of \[C{{N}^{+}}\]

Answer 1

Hint: We should know that \[C{{N}^{+}}\] which is a Cyanide radical (which is also called as nitride carbon (1+)) is a diatomic molecule. And for a bond order measurement, we need to enumerate the number of electrons involved in a particular bond in a molecule.

Complete step by step answer:
> It is highly imperative for you to understand the structure before finding out the bond order for a particular molecule.
> Bond order as we all should know or perhaps know is the measurement of the number of electrons involved in bonds between two atoms in a molecule. It primarily indicates the stability of a chemical bond.
> We should also know in this context the bond strength is directly proportional to the bond order of the molecule.
> There are multiple ways to depict a chemical compound through various theories such as Molecular orbital theory or Valence bond theory. But for the sake of understanding the solution, let us explore the solution through a typical Lewis Structure which is shown below:
${{C}^{+}}\equiv \underset{{}}{\overset{..}{\mathop{N}}}\,$
> We can also look at the molecular orbital diagram of the given molecule. i.e.

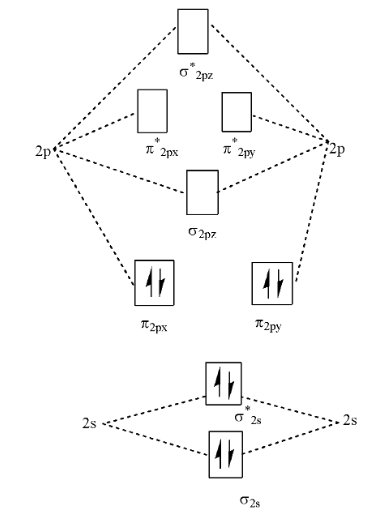
> Additionally to this chemical structure, we should know that Carbon has 6 electrons and Nitrogen has 7 electrons. We also need to consider a -1 for a positive charge on the cyanide radical. Hence the number of electrons in the given structure is: 6+7-1 which is 12 electrons.
> Now there is a trick involved here, that any species with 14 electrons will have a bond order of 3. For every increase or decrease of 2 electrons, the bond order decreases by 1. So, for our problem, we have a number of electrons equal to 12, hence the bond order we would have for the Cyanide radical would be 2.
- The Bond order for \[C{{N}^{+}}\] is 2.

Note:
1- Now, there are different ways through which you could come to your solution. The other elaborate way to do this is through Molecular Orbital Theory, in such a case you need to calculate the number of bonding electrons as well as the number of anti bonding electrons.
2- The formula would be:
\[\frac{(number\_Bonding\_electron)+(number\_antibonding\_electron)}{2}\]
Where antibonding electrons are the one which are outside the region between two nuclei.