
What is the exact value of
Answer
377.1k+ views
Hint: Here we are asked to find the value of the secant of angle
Complete answer:
We aim to find the value of
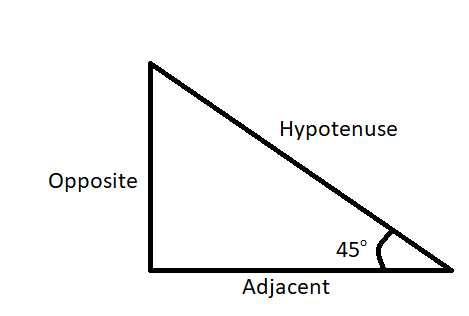
First of all, we have to look at the values of
From our trigonometric knowledge, we know that the secant function is also the reciprocal of the cosine function.
Hence, we can write
Here we are given
To find the value of
Therefore, we get,
We know that
Hence substituting the value:
Therefore the exact value of
Additional Information:
Trigonometry values of different ratios, which include, sine, cosine, tangent, secant, cotangent and cosecant deal with the measurement of lengths and angles of the right-attitude triangle. The values of trigonometric functions are commonly used to solve trigonometry troubles. Trigonometry deals with the measurement of angles and troubles related to angles. The time period trigonometry is derived from a Latin word. Trigonometric formulation, symptoms are widely used within the area of mathematics.
Note:
Trigonometry values are all approximately the observations of well-known angles for a given triangle with respect to trigonometric ratios. The word ‘trigon’ means triangle and ‘matron’ means ‘size’. It’s one of the primary concepts and part of geometry, in which the relationship between angles and aspects of a triangle is defined. Trigonometry is an essential part of arithmetic and is widely utilized in fixing hassle. A thorough understanding of trigonometric formulas is a vital part of fixing such troubles.
Complete answer:
We aim to find the value of

First of all, we have to look at the values of
From our trigonometric knowledge, we know that the secant function is also the reciprocal of the cosine function.
Hence, we can write
Here we are given
To find the value of
Therefore, we get,
We know that
Hence substituting the value:
Therefore the exact value of
Additional Information:
Trigonometry values of different ratios, which include, sine, cosine, tangent, secant, cotangent and cosecant deal with the measurement of lengths and angles of the right-attitude triangle. The values of trigonometric functions are commonly used to solve trigonometry troubles. Trigonometry deals with the measurement of angles and troubles related to angles. The time period trigonometry is derived from a Latin word. Trigonometric formulation, symptoms are widely used within the area of mathematics.
Note:
Trigonometry values are all approximately the observations of well-known angles for a given triangle with respect to trigonometric ratios. The word ‘trigon’ means triangle and ‘matron’ means ‘size’. It’s one of the primary concepts and part of geometry, in which the relationship between angles and aspects of a triangle is defined. Trigonometry is an essential part of arithmetic and is widely utilized in fixing hassle. A thorough understanding of trigonometric formulas is a vital part of fixing such troubles.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




