Question

What is the inverse of \[\sec \]\[?\]

Answer 1

Hint: To get the answer of this question you should know about the basics of the trigonometric functions and their concepts should be clear. Firstly do not get confused with the terms reciprocal and inverse they both are different terms and their functions are also different. So understand these entire concepts and get the answer.

Complete step-by-step answer:
There are in total six trigonometric functions and they are sine, cosine, tangent, secant and cosecant. Let us have a look at the secant function of trigonometry to know the answer.
Let us consider the right angled triangle,

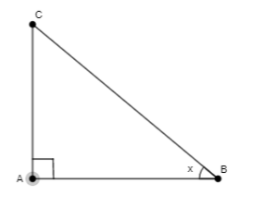
We know that the secant or in short sec is the ratio of the length of the hypotenuse and the length of the base of the right angle triangle. According to the diagram,
\[\sec =\dfrac{Hypotenuse}{Base}\]
\[\Rightarrow \sec x=\dfrac{BC}{AB}\]
As we know that secant is the reciprocal of the cosine function that is cosine is the ratio of length of the base and the length of the hypotenuse of the right angled triangle.
So do not get confused between the reciprocal and the inverse of the trigonometric function. The answer for this question is not cosine. Because it is the reciprocal not the inverse of secant. So now let us know what is the inverse of the trigonometric function.
The inverse of the trigonometric function means that the function which performs exactly the reverse work of that particular function. Now let us try to understand the meaning of this whole statement. The secant function gives the value at some angle i.e. secant of that angle will give some particular value. So basically this is a secant function. But the inverse of the secant function means that the inverse of the secant function of that particular value will give the angle then it is known as the inverse of the secant.
Now let us understand this with the help of an example.
The value of the secant function at \[{{90}^{0}}\] is \[0\]. Mathematically it is represented as
\[\sec {{90}^{0}}=0\]
Now if we ask the secant inverse of \[0\]then we will get \[{{90}^{0}}\]as our answer.
\[{{\sec }^{-1}}0={{90}^{0}}\]
The inverse of the trigonometric functions have the same name only the difference is \['arc'\]is present before the name of the function.
Hence we can conclude that the answer to the given question is \[arcsec\].
So, the correct answer is “\[arcsec\]”.

Note: In mathematics, inverse trigonometric functions are also known as the arcus functions or they are also known as the anti-trigonometric functions. There are a lot of applications of inverse trigonometry like it has its application in engineering, used in physics, geometry and for navigation purposes.