
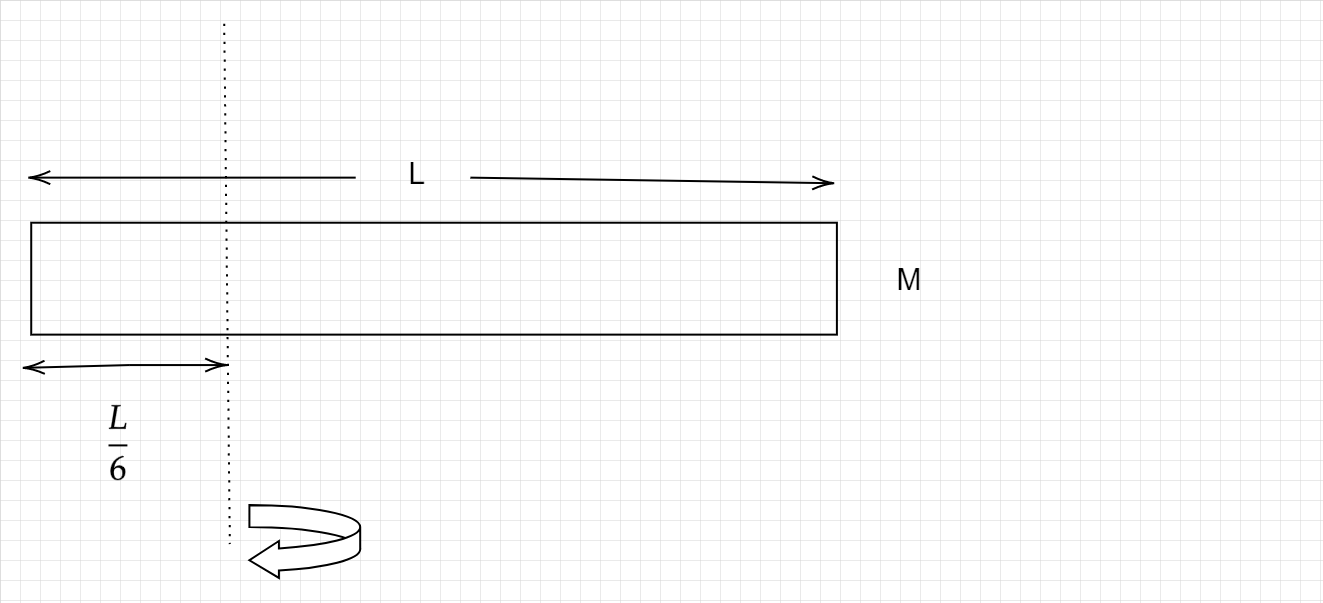
What is the MOI of the following:-

Answer
418.5k+ views
Hint: First taking the moment of inertia formula and defining the initial variables/terms with some basic knowledge. Then, assuming the axis to be in center first and solving the equation as when the object is rotating on the axis. Afterwards, solving the equation when the axis is further than center as described in the diagram.
Complete step-by-step solution:
The moment of inertia (MOI) in the diagram,
The formula of MOI is,
Where, m is sum of the product of mass, r= distance from the axis of rotation, and integral form:
The role of MOI is the same as the role of mass in linear motion.
Taking mass as M and length as L, distributed mass as dm and distributed length as dl
Assuming the axis to be the center of the rectangle object, it has a uniform speed. Thus, the density remains unchanged.
Moving
When the mass is distributed in more complicated way at different distances from the rotation axis:
Replacing the value of dm in this formula:
Changing
Applying integration to it
Terminating denominator
Thus, deriving this formula
Where
According to parallel axis theorem,
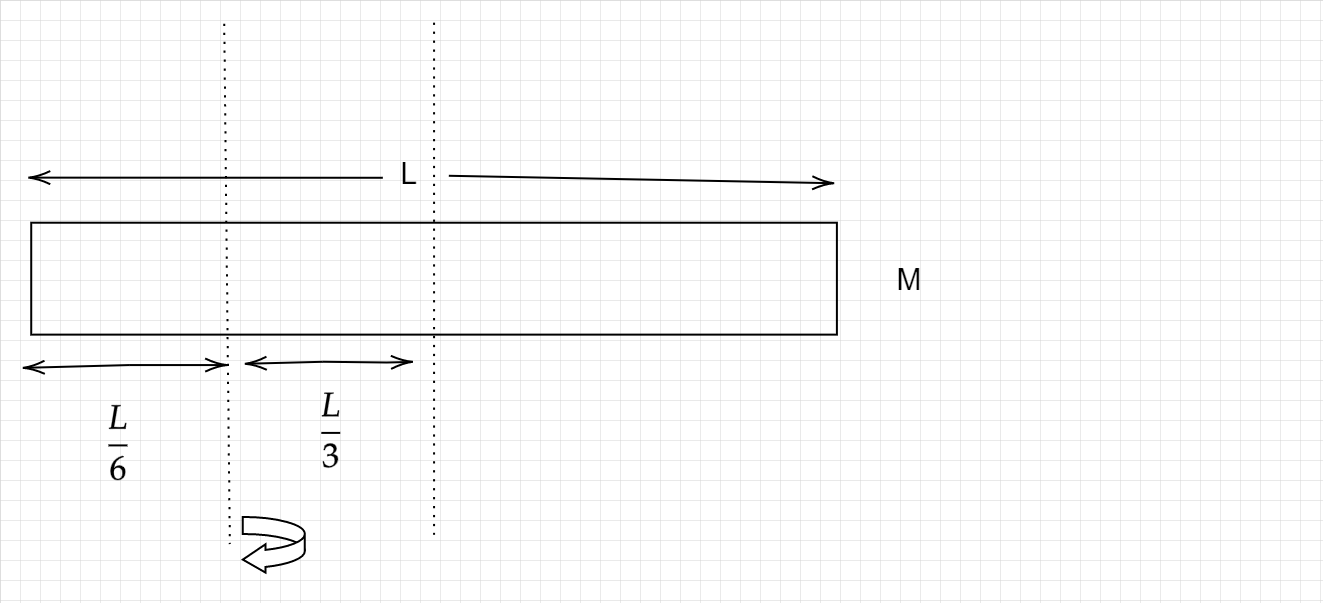
In a given rotation axis direction, the moment of inertia increases as the axis becomes further than the center. Thus, the moment of inertia of the rectangle object when the axis is some distance further than center then it’s MOI of center axis with MOI of axis of distance d from center. So the formula is
Where d is the distance between the center axis and given axis. Thus, d
And mass is M same as above
Putting, MOI of center axis.
Solving the above equation, we get:
The moment of inertia in the rectangle object is
Note: The moment of inertia depends on the following factors like: The density of the material, Shape and size of the body, Axis of rotation (distribution of mass relative to the axis). Moment of inertia is usually specified with respect to a chosen axis of rotation. It mainly depends on the distribution of mass around an axis of rotation.
Complete step-by-step solution:
The moment of inertia (MOI) in the diagram,
The formula of MOI is,
Where, m is sum of the product of mass, r= distance from the axis of rotation, and integral form:
The role of MOI is the same as the role of mass in linear motion.
Taking mass as M and length as L, distributed mass as dm and distributed length as dl
Assuming the axis to be the center of the rectangle object, it has a uniform speed. Thus, the density remains unchanged.
Moving
When the mass is distributed in more complicated way at different distances from the rotation axis:
Replacing the value of dm in this formula:
Changing
Applying integration to it
Terminating denominator
Thus, deriving this formula
Where
According to parallel axis theorem,

In a given rotation axis direction, the moment of inertia increases as the axis becomes further than the center. Thus, the moment of inertia of the rectangle object when the axis is some distance further than center then it’s MOI of center axis with MOI of axis of distance d from center. So the formula is
Where d is the distance between the center axis and given axis. Thus, d
And mass is M same as above
Putting, MOI of center axis.
Solving the above equation, we get:
The moment of inertia in the rectangle object is
Note: The moment of inertia depends on the following factors like: The density of the material, Shape and size of the body, Axis of rotation (distribution of mass relative to the axis). Moment of inertia is usually specified with respect to a chosen axis of rotation. It mainly depends on the distribution of mass around an axis of rotation.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




