Question

What is the range of function \[y = x\] ?

Answer 1

Hint: Here, we need to check the range of the given function, \[y = x\]. A function's range is the set of all possible \[y\] , values. All potential data, or \[x\] , values make up the domain. Both the range and the domain of \[y = x\] are all real numbers. We use the Set-Builder Notation is the mathematical notation for describing a set by stating all the properties that the elements in the set must satisfy. The set is written in this form: \[\{ variable|condition1,{\text{ }}condition2,.\} \] Where, the middle bar can be read as ‘such that’.

Complete step by step solution:
In the given problem,
The range of function is \[y = x\]
To determine the range, we can plot the graph.

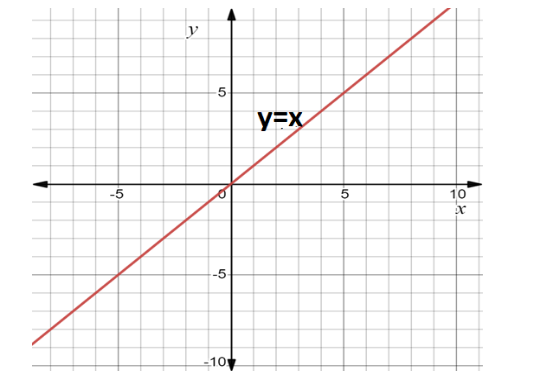
Here, the domain of the expression is all real numbers, \[\mathbb{R}\] except where the expression is undefined. Because, there is no real number that makes the expression undefined.
Interval Notation:
 \[( - \infty ,\infty )\]
Set-Builder Notation:
 \[\{ x|x \in \mathbb{R}\} \]
The range is a set of all valid \[y\] values. To determine the range, we can plot the graph.
Interval Notation:
 \[\left( { - \infty ,\infty } \right)\]
Set-Builder Notation:
 \[\{ y|y \in \mathbb{R}\} \]
Therefore, determine the domain and range.
Domain: \[\left( { - \infty ,\infty } \right),\{ x|x \in \mathbb{R}\} \]
Range: \[\left( { - \infty ,\infty } \right),\{ y|y \in \mathbb{R}\} \]

Note: We note that the function is a relationship between two variables in which the value of one variable, known as the independent variable, determines the value of the other variable, known as the dependent variable. The domain of a function is given up of all of the independent variable values that result in a defined function, and the range of the function also consists of all of the values of the dependent variable that the domain of the function creates. There are no limits in all sorts of negative and positive \[x\] and \[y\] values you can use. As a consequence, in interval notation \[( - \infty ,\infty )\] is the range. \[( - \infty ,\infty )\] is the domain. Since, infinity isn't a number, it's enclosed in round brackets \[\left( {\text{ }} \right),\] the function cannot be defined there.