Question

What is the slope of the line y=-3?

Answer 1

Hint: We need to find the slope of the line y=-3. We start to solve the given question by plotting the graph of the line y=-3. Then, we find the slope of the given line using the slope formula given by $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ to get the desired result.

Complete step-by-step answer:
We are given a line equation and are asked to find the slope of the given line equation. We will be solving the given question using the slope formula $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ .
The slope of a straight line is used to determine the steepness of the line. It is usually the ratio of the amount y increases to the amount x increases.
The slope of the line is usually denoted by a variable m.
It is given as follows,
$\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Here,
$\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ are the first and second coordinates in the line.
According to the question,
We need to find the slope of the line y=-3.
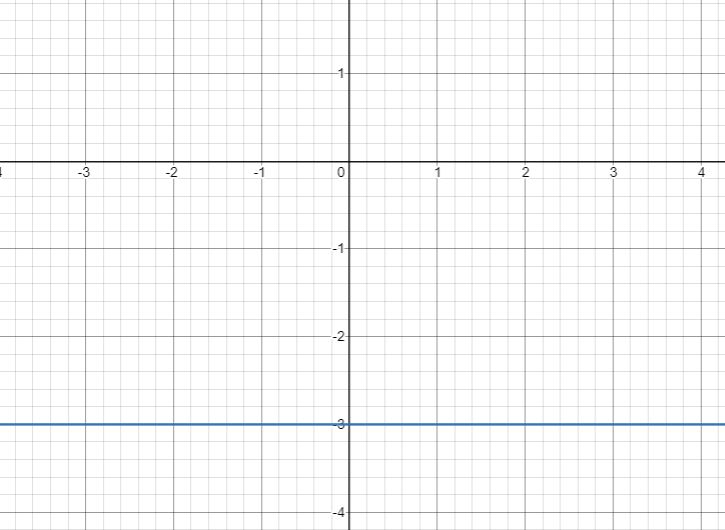
The graph of the line y=-3 is represented as follows,

From the graph,
We observe that the line y=-3 does not pass through the horizontal axis or the x-axis.
From the above,
The value of y is always equal to -3 for any values of the horizontal coordinates.
Following the same, we get,
${{y}_{2}}=-3$
${{y}_{1}}=-3$
${{x}_{1}}={{x}_{1}}$
${{x}_{2}}={{x}_{2}}$
Substituting the above values of coordinates in the slope formula, we get,
$\Rightarrow m=\dfrac{\left( -3-\left( -3 \right) \right)}{{{x}_{2}}-{{x}_{1}}}$
Simplifying the above equation, we get,
$\Rightarrow m=\dfrac{-3+3}{{{x}_{2}}-{{x}_{1}}}$
$\therefore m=0$

The slope of the line y=-3 is zero.

Note: The slope of the graph can be alternatively found as follows,
The general equation of the straight line is given by $y=mx+c$
Here,
m = slope
Representing the line y=-3 in the form of y=mx+c, we get,
$\Rightarrow y=0x+\left( -3 \right)$
$\therefore y=0x-3$
Comparing the above equation with the standard line equation, the slope of the line y=-3 is zero.