Question

What is the value of \[\cos 180{}^\circ \]?

Answer 1

Hint: When we work with triangles in trigonometry, then our task becomes easier and it becomes easy for us to solve our question. The Cartesian system should be known to you and you should also know that there are six functions for angles of trigonometry which are sine, cosine, secant, cosecant, tangent, cotangent.

Complete step-by-step answer:
Trigonometry is the study of measurements of triangles which deals with the length, height, and angles of the triangle. The trigonometry functions have a different application in the real world. In various fields like engineering, architecture, satellite navigation, development of waves, etc.
Trigonometry is the branch of mathematics that deals with various functions of angles and there are six different functions of angles which are sine, cosine, tangent, cotangent, secant, and cosecant.
All the different angles of trigonometry are there in the Cartesian plane which consists of four quadrants. In the first quadrant of the Cartesian system, all the angles will have a positive value. In the second quadrant, the value of angles of sine and cosecant will be positive. In the third quadrant, the value of tangent and cotangent will be positive, and in the fourth quadrant, cosine and secant will be positive.
The value of \[\cos 180{}^\circ \] or the value of \[\cos \pi \] can be represented in terms of different angles like \[0{}^\circ ,90{}^\circ \]and \[270{}^\circ \]. The Cartesian coordinate system contains angles from \[0{}^\circ \] to \[360{}^\circ \]. The first quadrant contains the angles between \[0{}^\circ <\theta <90{}^\circ \]. The second quadrant contains the angle between \[90{}^\circ <\theta <180{}^\circ \]. The third quadrant contains the angle between \[180{}^\circ <\theta <270{}^\circ \] and the fourth quadrant contains angle from \[270{}^\circ <\theta <360{}^\circ \].
There is a unit circle in which the cartesian plane is divided into four quadrants.

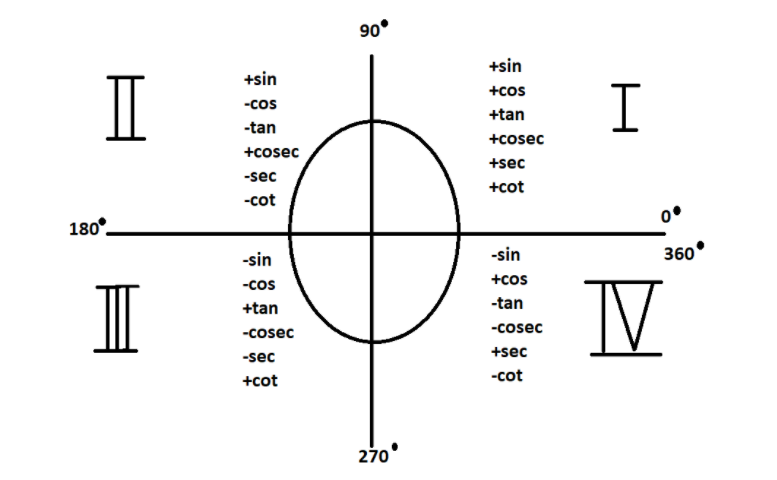
From the above diagram we can figure out the following:
\[\]
So to find the value of \[\cos 180{}^\circ \]we can write as
\[\cos \pi \]=\[\cos \left( \dfrac{3\pi }{2}-\dfrac{\pi }{2} \right)\]
\[\cos \pi \]=\[-\sin \dfrac{\pi }{2}\] ( as we know that \[\cos \left( \dfrac{3\pi }{2}-\theta \right)=-\sin \theta \])
We know that the value of \[\sin \dfrac{\pi }{2}=1\]
On Substituting the obtained value in the above relation, we get
 \[\cos \pi \]= \[-1\]
So, the value of \[\cos 180{}^\circ \] is \[-1\].
So, the correct answer is “-1”.

Note: The angles of trigonometry are associated with the base, height, and hypotenuse of a triangle, like a sine angle represents the ratio between height and hypotenuse of the triangle. Cosine angle represents the ratio between the base and hypotenuse of a triangle whereas tangent angle represents the ratio between height and base of the triangle.