Question

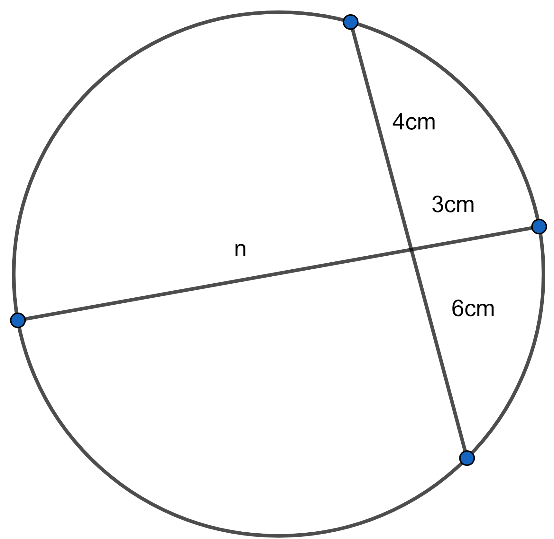
What is the value of n?

Answer 1

Hint: This is the question of intersecting chords. This type of question describes the relation between the four line segments created by two intersecting chords inside a circle. The product of the line segments on each chord will be equal.

Complete step by step solution:

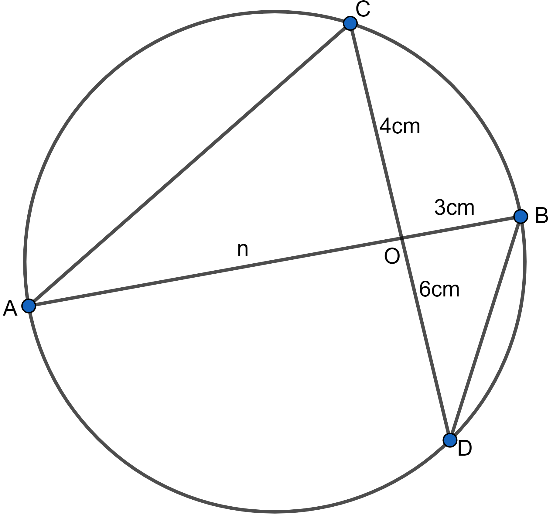
Here in the given figure, we can see that there are two chords intersecting each other.
We can see that in one chord which is having the length 10cm and due to intersection the line segments are 4cm and 6cm in length.
Now, In the second chord one segment is having length 3cm and the other line segment is denoted by (n), and we have to take out the value of (n) as asked in the question.
Now using formula;
(Product of the line segment of chord 1= Product of the line segment of chord 2) ………………………… (i)
This formula can be proven using the similar triangle. Considering triangles \[\Delta AOC\] and \[\Delta BOD\].
Equation (i), can be written as;
\[\left( AO\times OB=CO\times OD \right)\]………………………. (ii)
Putting values as given;
\[\Rightarrow n\times 3cm=4cm\times 6cm\] …………………………… (iii)
In equation (iii), Divide both sides by (3);
\[\Rightarrow \left( n\times 3cm\times \dfrac{1}{3cm}=4cm\times 6cm\times \dfrac{1}{3cm} \right)\]
\[\Rightarrow n=4cm\times 2cm\]
\[\Rightarrow n=8cm\]
Hence, we concluded the length of the line segment AO.
Thus, the value of (n) will be 8cm.

Note: We should know the concept of similar triangles. Properties of similar triangles. Basic knowledge of circle is necessary like we should identify chords, secant, tangent etc.