Question

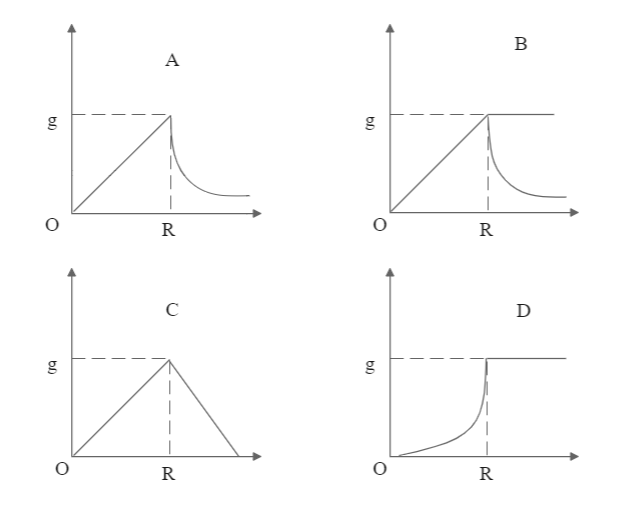
Which graph shows the correct variation of g with height or depth r, where R is the radius of the Earth?

Answer 1

Hint
Gravitational acceleration depends on the position where it is acting. As we move deeper and deeper inside the earth, the gravitational pull and hence, the acceleration will increase linearly.

Complete step by step answer
The acceleration of a body also changes with altitude. The change in gravitational acceleration with distance from the centre of Earth follows an inverse-square law relation. This implies that gravitational acceleration is inversely proportional to the square of the distance from the centre of Earth. That’s why for an object placed at some height h from the surface of the Earth is less than what the object will experience when at the surface.
For depths lower than the radius of the earth, the gravitational acceleration is given as:
$\Rightarrow g\alpha (R - d)$
where d is the depth from the surface of earth. So, for a distance from the centre of the Earth at O to the surface at R, the value of gravitational acceleration will increase linearly. This means that the graph will have a straight line for this portion. This property is followed by the graphs A, B and C.
We also know that for heights above the surface of the Earth, the gravitational acceleration follows:
$\Rightarrow g\alpha \dfrac{1}{{{R^2}}}$
For this dependency, an increasing parabola will be formed in the latter half of the graph. Graph B denotes uniform dependency, while graph C denotes a linearly decreasing relation. So, these are not correct. We can see that in graph A, the curve of the parabola is increasing with distance.
Hence, the correct answer is option (A).

Note
Apart from benefits in the physical sciences, the acceleration due to gravity is also helpful in maintaining the structure of our body. It plays an important role in the proper circulation of blood, and the load that our bones can take.