Question

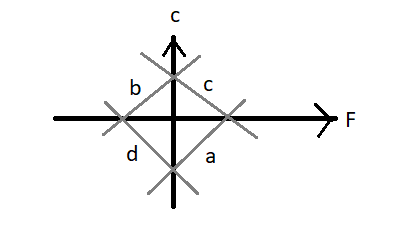
Which of the curves in the figure represents the relation between Celsius and Fahrenheit temperature?

$(A)$ Curve a
$(B)$Curve b
$(C)$Curve c
$(D)$Curve d

Answer 1

Hint : Here, we’ll proceed by writing down the relation between Celsius and Fahrenheit temperature scales. After that, compare this equation with the general equation of a straight line. Then we will calculate the slope using those two equations and see which slopes in the diagram match it.

Formula used:
\[F = \dfrac{9}{5} \times C + 32\]
\[y = mx + c\]
\[m\] denotes the slope of the straight line and \[c\] denotes the intercept of the straight line on the y-axis

Complete step-by-step solution:
According to the relation between Celsius and Fahrenheit temperature scales, we get
\[F = \dfrac{9}{5} \times C + 32 - - - - - - \left( 1 \right)\]
We all know that the general equation of any straight line is given by
\[y = mx + c - - - - - - \left( 2 \right)\]
Where \[m\] denotes the slope of the straight line and \[c\] denotes the intercept of the straight line on the y-axis
Since in the given figure, it’s clear that the x-axis corresponds to the Fahrenheit temperature scale and therefore the y-axis corresponds to the Celsius temperature scale
By rearranging the equation (1), we get
\[ \Rightarrow F - 32 = \dfrac{9}{5} \times C\]
\[ \Rightarrow C = \dfrac{5}{9} \times \left( {F - 32} \right)\]
\[ \Rightarrow C = \left( {\dfrac{5}{9}} \right)F - \dfrac{5}{9} \times 32\]
\[C = \left( {\dfrac{5}{9}} \right)F - \dfrac{{160}}{9}. - - - - - - \left( 3 \right)\]
By comparing equation (2) with equation (3), we can say that the relation between the Celsius and Fahrenheit temperature is a straight line having a slope of \[\dfrac{5}{9}\] and y-intercept as\[\dfrac{{ - 160}}{9}\]. This suggests that the straight line representing the relation between the Celsius and Fahrenheit temperature has a positive slope and negative intercept. Therefore, the specified curve representing the relation between Celsius and Fahrenheit is curve \[a\] which is lying within the fourth quadrant.
So, the correct answer is “Option A”.

Note: In this particular problem, it’s important to know the various characteristics of the straight lines lying in the figure given. The curve \[a\] lying in the fourth quadrant have the positive slope and negative intercept, the curve \[b\] lying in the second quadrant have a positive slope and positive intercept, the curve \[c\] lying in the first quadrant has a negative slope and positive intercept, and the curve \[d\] lying in the third quadrant have a negative slope and negative intercept.