Question

Which of the following are equiangular and equilateral polygons?
A. Square
B. Rhombus
C. Kite
D. None of these

Answer 1

Hint: To answer this question, we need to know what is meant by equiangular polygons and equilateral polygons. Then we can classify the polygons given in the options to find the one which is both equilateral and equiangular.

Complete step-by-step answer:
A two-dimensional closed shape which is made using only straight lines is known as a polygon.
When a polygon has all the sides which are equal or congruent then the polygon is said to be an equilateral polygon. An example of an equilateral polygon includes rhombus whose all sides are equal.
When a polygon has all its interior angles equal or congruent then the polygon is said to be an equiangular polygon. An example of an equiangular polygon includes a rectangle whose all interior angles are equal to ${90^ \circ }$ .
When a polygon satisfies the conditions to be an equiangular polygon as well as an equilateral polygon, then the polygon is said to be a regular polygon. An example of a regular polygon is a square whose all sides are equal and all interior angles are always equal to ${90^ \circ }$ .
The question asks us for a polygon which is both equiangular and equilateral i.e. a regular polygon.
A square always has all its sides to be equal and its interior angles are always equal to ${90^ \circ }$ , satisfying the conditions to be an equiangular as well as an equilateral polygon. Thus, we can say that square is a regular polygon
                                              

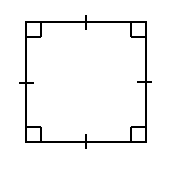
Therefore, option (a) satisfies being an equiangular and equilateral polygon
A rhombus has all sides which are always equal to each other but the interior angles of a rhombus are not equal. The opposite angles are equal to each other but the adjacent angles are not equal to each other. Thus, a rhombus is equilateral but not equiangular.
A special case of rhombus when all its sides and all its angles are equal is a square. But in this question we are not looking at special cases, rather the general cases.
                                           

Therefore, option (b) does satisfy being equilateral but does not satisfy being equiangular.
A kite is a polygon with two of its adjacent sides being equal or congruent to each other but are not equal to the other two. The angles between the two congruent sides are known as the vertex angles whereas the angles between the non-congruent sides are known as the non-vertex angles. The non-vertex angles of a kite are equal to each other but the vertex angles are never equal to each other and the non-vertex angles. Thus, in a kite neither all its sides are equal nor its interior angles are equal. This implies that a kite is neither equilateral nor equiangular.
                                                 

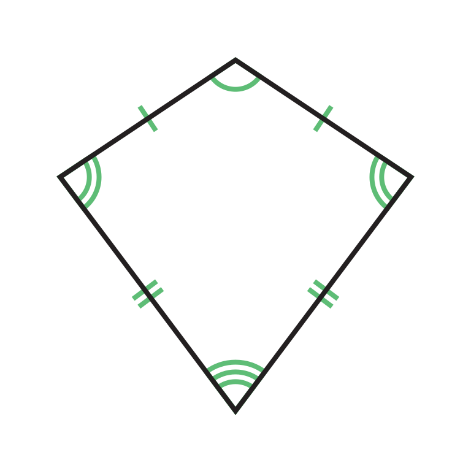
Therefore, option (c) does not satisfy being equilateral or equiangular.
Since, square is a polygon that satisfies being both equiangular and equilateral, we can rule out the option (d) which states that none of the options are right.

Therefore, option (a) square is the correct answer.

Note:
Polygons are also classified based on the number of sides present in the polygons. A three-sided polygon is known as a triangle, four-sided polygon is a quadrilateral, five-sided is pentagon, six-sided is hexagon, seven-sided is heptagon, eight-sided is octagon, nine-sided is nonagon, ten-sided is decagon and so on.