Answer
404.1k+ views
Hint:Clausius equality and inequality are two terms which come into picture while finding the closed integral of the ratio of change of heat to the temperature of a thermodynamic system.
Complete step by step answer:
Assume:
\[d{Q_1}\] is the amount of heat supplied to both the heat engines.
\[d{Q_2}\] and \[d{Q_2}^\prime \] be the amount of heat rejected to the sink by reversible and irreversible heat engines respectively.
\[{T_1}\] and \[{T_2}\] are the temperatures of the heat source and sink respectively.
\[d{W_R}\] and \[d{W_I}\] are the work produced by reversible and irreversible heat engines respectively.
\[{\rm{H}}{{\rm{E}}_R}\] and \[{\rm{H}}{{\rm{E}}_I}\] represents reversible and irreversible heat engine respectively.
Consider two heat engines, one is reversible heat engine and other is irreversible heat engine and both of them are operating between same temperature levels \[{T_1}\] and \[{T_2}\].
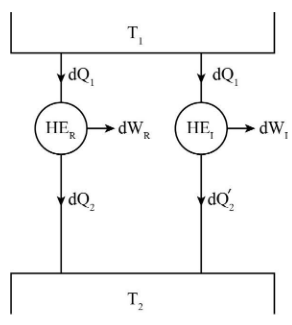
Carnot theorem states that if many heat engines are working under constant temperature source and constant temperature sink then the efficiency of reversible heat engines will always be high if compared to irreversible heat engines.
\[{\eta _R} > {\eta _I}\]……(1)
The efficiencies of reversible and irreversible heat engines as shown in figure are given as
\[{\eta _R} = \dfrac{{d{W_R}}}{{d{Q_1}}}\]
\[\Rightarrow{\eta _I} = \dfrac{{d{W_I}}}{{d{Q_1}}}\]
Substitute \[\dfrac{{d{W_R}}}{{d{Q_1}}}\] for \[{\eta _R}\] and \[\dfrac{{d{W_I}}}{{d{Q_1}}}\] for \[{\eta _I}\] in equation (1).
\[\dfrac{{d{W_R}}}{{d{Q_1}}} > \dfrac{{d{W_I}}}{{d{Q_1}}}\]……(2)
Using first law of thermodynamics for \[{\rm{H}}{{\rm{E}}_R}\] and \[{\rm{H}}{{\rm{E}}_I}\] respectively.
\[
d{W_R} = d{Q_1} - d{Q_2}\\
\Rightarrow d{W_I} = d{Q_1} - d{Q_2}^\prime
\]
Substitute \[d{Q_1} - d{Q_2}\] for \[d{W_R}\] and \[d{Q_1} - d{Q_2}^\prime \] for \[d{W_I}\] in equation (2).
\[
\dfrac{{d{Q_1} - d{Q_2}_{}}}{{d{Q_1}}} > \dfrac{{d{Q_1} - d{Q_2}^\prime }}{{d{Q_1}}}\\
\Rightarrow - \dfrac{{d{Q_2}}}{{d{Q_1}}} > - \dfrac{{d{Q_2}^\prime }}{{d{Q_1}}}\\
\Rightarrow\dfrac{{d{Q_2}}}{{d{Q_1}}} < \dfrac{{d{Q_2}^\prime }}{{d{Q_1}}}\\
\Rightarrow d{Q_2} < d{Q_2}^\prime
\]……(3)
Expanding the relation \[\oint {\dfrac{{dQ}}{T}} \] for irreversible heat engines.
\[\oint {\dfrac{{dQ}}{T}} = \dfrac{{d{Q_2}}}{{{T_1}}} - \dfrac{{d{Q_2}^\prime }}{{{T_2}}}\]
From equation (3), it is clear that the heat rejected by reversible heat engines is less than the heat rejected by the irreversible heat engine. Hence the term \[\left( {\dfrac{{d{Q_2}}}{{{T_1}}} - \dfrac{{d{Q_2}^\prime }}{{{T_2}}}} \right)\] becomes less than zero.
$\oint {\dfrac{{dQ}}{T}} = \dfrac{{d{Q_2}}}{{{T_1}}} - \dfrac{{d{Q_2}^\prime }}{{{T_2}}}\\
\Rightarrow\oint {\dfrac{{dQ}}{T}} < 0
$
Writing the above equation in per unit mass form.
$\oint {\dfrac{{dq}}{T}} < 0$
Therefore the expression for Clausius inequality is given by $\oint {\dfrac{{dq}}{T}} < 0$ and the option (A) is correct.
Note:: We have to note that the term $\oint {\dfrac{{dq}}{T}} $ is less than or equal to zero to make the system feasible in nature but if it became more than zero then it can be said that system is impossible in nature.
Complete step by step answer:
Assume:
\[d{Q_1}\] is the amount of heat supplied to both the heat engines.
\[d{Q_2}\] and \[d{Q_2}^\prime \] be the amount of heat rejected to the sink by reversible and irreversible heat engines respectively.
\[{T_1}\] and \[{T_2}\] are the temperatures of the heat source and sink respectively.
\[d{W_R}\] and \[d{W_I}\] are the work produced by reversible and irreversible heat engines respectively.
\[{\rm{H}}{{\rm{E}}_R}\] and \[{\rm{H}}{{\rm{E}}_I}\] represents reversible and irreversible heat engine respectively.
Consider two heat engines, one is reversible heat engine and other is irreversible heat engine and both of them are operating between same temperature levels \[{T_1}\] and \[{T_2}\].

Carnot theorem states that if many heat engines are working under constant temperature source and constant temperature sink then the efficiency of reversible heat engines will always be high if compared to irreversible heat engines.
\[{\eta _R} > {\eta _I}\]……(1)
The efficiencies of reversible and irreversible heat engines as shown in figure are given as
\[{\eta _R} = \dfrac{{d{W_R}}}{{d{Q_1}}}\]
\[\Rightarrow{\eta _I} = \dfrac{{d{W_I}}}{{d{Q_1}}}\]
Substitute \[\dfrac{{d{W_R}}}{{d{Q_1}}}\] for \[{\eta _R}\] and \[\dfrac{{d{W_I}}}{{d{Q_1}}}\] for \[{\eta _I}\] in equation (1).
\[\dfrac{{d{W_R}}}{{d{Q_1}}} > \dfrac{{d{W_I}}}{{d{Q_1}}}\]……(2)
Using first law of thermodynamics for \[{\rm{H}}{{\rm{E}}_R}\] and \[{\rm{H}}{{\rm{E}}_I}\] respectively.
\[
d{W_R} = d{Q_1} - d{Q_2}\\
\Rightarrow d{W_I} = d{Q_1} - d{Q_2}^\prime
\]
Substitute \[d{Q_1} - d{Q_2}\] for \[d{W_R}\] and \[d{Q_1} - d{Q_2}^\prime \] for \[d{W_I}\] in equation (2).
\[
\dfrac{{d{Q_1} - d{Q_2}_{}}}{{d{Q_1}}} > \dfrac{{d{Q_1} - d{Q_2}^\prime }}{{d{Q_1}}}\\
\Rightarrow - \dfrac{{d{Q_2}}}{{d{Q_1}}} > - \dfrac{{d{Q_2}^\prime }}{{d{Q_1}}}\\
\Rightarrow\dfrac{{d{Q_2}}}{{d{Q_1}}} < \dfrac{{d{Q_2}^\prime }}{{d{Q_1}}}\\
\Rightarrow d{Q_2} < d{Q_2}^\prime
\]……(3)
Expanding the relation \[\oint {\dfrac{{dQ}}{T}} \] for irreversible heat engines.
\[\oint {\dfrac{{dQ}}{T}} = \dfrac{{d{Q_2}}}{{{T_1}}} - \dfrac{{d{Q_2}^\prime }}{{{T_2}}}\]
From equation (3), it is clear that the heat rejected by reversible heat engines is less than the heat rejected by the irreversible heat engine. Hence the term \[\left( {\dfrac{{d{Q_2}}}{{{T_1}}} - \dfrac{{d{Q_2}^\prime }}{{{T_2}}}} \right)\] becomes less than zero.
$\oint {\dfrac{{dQ}}{T}} = \dfrac{{d{Q_2}}}{{{T_1}}} - \dfrac{{d{Q_2}^\prime }}{{{T_2}}}\\
\Rightarrow\oint {\dfrac{{dQ}}{T}} < 0
$
Writing the above equation in per unit mass form.
$\oint {\dfrac{{dq}}{T}} < 0$
Therefore the expression for Clausius inequality is given by $\oint {\dfrac{{dq}}{T}} < 0$ and the option (A) is correct.
Note:: We have to note that the term $\oint {\dfrac{{dq}}{T}} $ is less than or equal to zero to make the system feasible in nature but if it became more than zero then it can be said that system is impossible in nature.
Recently Updated Pages
How many sigma and pi bonds are present in HCequiv class 11 chemistry CBSE

Why Are Noble Gases NonReactive class 11 chemistry CBSE

Let X and Y be the sets of all positive divisors of class 11 maths CBSE

Let x and y be 2 real numbers which satisfy the equations class 11 maths CBSE

Let x 4log 2sqrt 9k 1 + 7 and y dfrac132log 2sqrt5 class 11 maths CBSE

Let x22ax+b20 and x22bx+a20 be two equations Then the class 11 maths CBSE

Trending doubts
Which are the Top 10 Largest Countries of the World?

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Difference Between Plant Cell and Animal Cell

Give 10 examples for herbs , shrubs , climbers , creepers

Change the following sentences into negative and interrogative class 10 english CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE



