Question

Which of the following graph depicts spring constant $ K $ versus length $ L $ of the spring correctly?
(A)

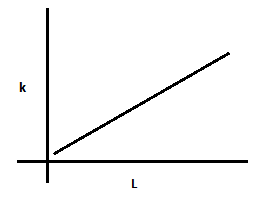
(B)

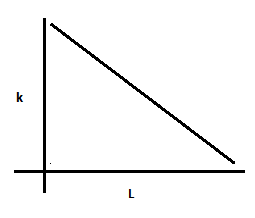
(C)

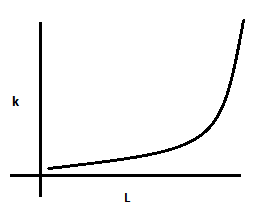
(D)

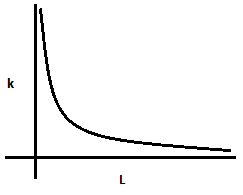
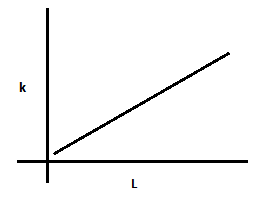
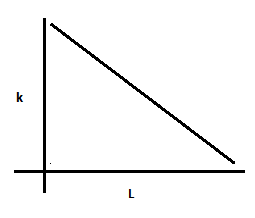
Answer 1

Hint :We will be using the concepts of Hooke’s law and the effect of some external force on a material and in this case it will be a spring.
(1) The Hooke’s Law:
 $ F=-kx $
Where $ F $ is the force, $ k $ is the spring constant and $ x $ is the displacement.
(2) The Young’s Modulus
 $ Y=\dfrac{stress}{strain} $

Complete Step By Step Answer:
As we all know that an ideal spring is remarkable within the sense that it's a system where the generated force is linearly dependent on how far it's stretched. Hooke’s law describes this behaviour. In order to increase a spring by an amount x from its previous position, one needs a force $ F $ which is decided by $ F=-kx $ .Hooke’s Law states that:
 $ F=-kx $
Here $ k $ is the spring constant, which may be a quality particular to every spring, and $ x $ is a distance the spring is stretched or compressed. The force $ F $ is definitely a restorative force and its direction is opposite (hence the minus sign) to the direction of the spring’s displacement.
Now, we define Young’s Modulus as the measurement of the ability of a material to withstand any change in its length when under linear tension or compression. We also refer to it as modulus of elasticity. The equation is given as
 $ \begin{align}
  & Y=\dfrac{stress}{strain} \\
 & \Rightarrow Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta L}{L}} \\
 & \Rightarrow Y=\dfrac{FL}{A\Delta L} \\
\end{align} $
Now, we calculate the spring constant using this equation.
 $ \Rightarrow F=\left( \dfrac{YA}{L} \right)\Delta L $
Here, the quantity in the brackets is equal to the spring constant if we compare this equation with the Hooke’s Law. And also the change in length $ \Delta L $ is equal to $ x $ .
Therefore,
 $ k=\dfrac{YA}{L} $
And hence we can say that the spring constant is inversely proportional to length of the spring. And therefore, our graph will be similar to that in option (D).
Hence, option (D) is the correct answer.

Note :
According to the solution we are deriving, the graph should be a straight line but there are many factors that affect the spring constant and hence, we end up with a curved graph. Also keep in mind that in a spring, the tension is applied linearly and hence Young’s Modulus.