Question

Which of the following graphs represents Boyles’s law? This question has multiple correct options.

Answer 1

Hint: We should recall the concepts of Boyle’s law. We should know the relationship between pressure and volume. Boyles’s law tells us about the change in volume when pressure is exerted by gas. It can be inversely proportional or directly proportional.

Complete step by step answer:
So, if we recall Boyle's law, we come to know that Boyle’s law is a gas law which states that the pressure exerted by a gas (of a given mass, kept at a constant temperature) is inversely proportional to the volume occupied by it. In other words, we can say that the pressure and volume of a gas are inversely proportional to each other as long as the temperature and the quantity of gas are kept constant.
For a gas, we can tell the relationship between volume and pressure (at constant mass and temperature). It can be mathematically expressed as follows:
P ∝ (\[\dfrac{1}{V}\]):- by this equation we can say that, P is the pressure exerted by the gas and V is the volume occupied by it. P is inversely proportional to V. This proportionality can be converted into an equation by adding a constant, k.
\[~\mathbf{P}=\mathbf{k}\times \left( \dfrac{1}{V} \right)\to \mathbf{PV}=\mathbf{k}\]
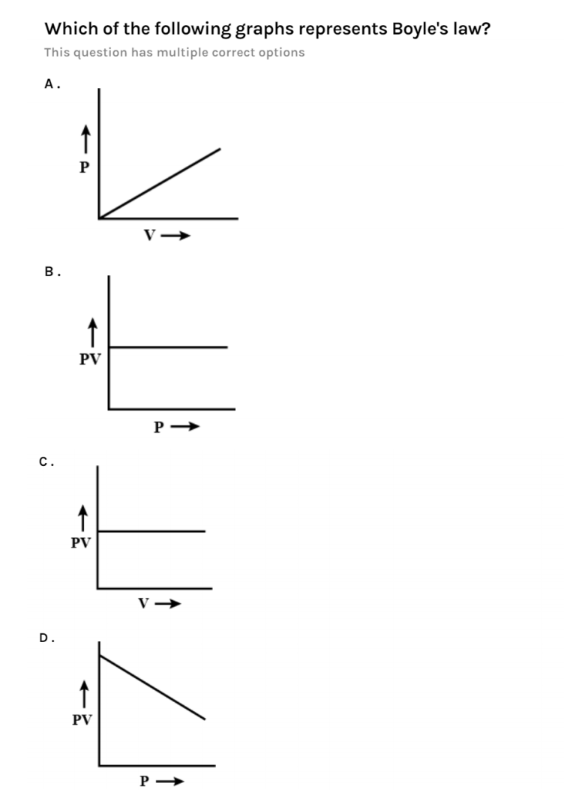
From the above equation, we came to know that the product of pressure and volume is always equals to constant k. So, if we observe the graph we came to know that the options B and C represent Boyle's law as PV= constant.
In both the options B and C, PV is behaving as constant just as in the equation. Now we will check other options also.
If we take option A, we see that as pressure is increasing proportional to volume. Graph is showing as pressure increases volume also increases uniformly. This graph is not a correct representation of Boyle’s law.
If we represent the equation from the graph represented in option A. It will look like this,$P\propto V$. So this is not Boyle’s law. So, option A is incorrect.
If we now come to option D, the graph in it states that the product of pressure and volume is not constant. If we look at the graph it is looking like a product of pressure and volume is decreasing with increasing pressure. This is not Boyle’s law. Because Boyle’s law states that the product of pressure and volume is constant.
So, option D is incorrect.
From the above discussion we came to know that the correct options of this question are option B and C. this is because Boyle's law states that product of pressure and volume is constant and these graphs also say that product of pressure and volume is constant whether we increase pressure or volume it will always remain constant.
​So, option B and C are correct.
Additional information:
There is a derivation of Boyle’s law that we should learn:
From Boyle's law we study, we can say that any change in the volume occupied by a gas (at constant quantity and temperature) will result in a change in the pressure exerted by it. In other words, we can say that the product of the initial pressure and the initial volume of a gas are equal to the product of its final pressure and final volume (at constant temperature and number of moles). This law can be expressed mathematically as follows:
\[\]\[{{P}_{1}}{{V}_{1}}=\text{ }{{P}_{2}}{{V}_{2}}\]

Where,
\[{{P}_{1}}\]= the initial pressure exerted by the gas.
\[{{V}_{1}}\]= the initial volume occupied by the gas.
\[{{P}_{2}}\]= the final pressure exerted by the gas.
\[{{V}_{2}}\] = the final volume occupied by the gas.
We had obtained this expression from the pressure-volume relationship given by Boyle’s law. For a fixed amount of gas kept at a constant temperature, PV = k. Therefore,
\[{{P}_{1}}{{V}_{1}}\] = k (initial pressure × initial volume)
\[{{P}_{2}}{{V}_{2}}\] = k (final pressure × final volume)
So, \[{{P}_{1}}{{V}_{1}}=\text{ }{{P}_{2}}{{V}_{2}}\]
We can learn more about Boyle’s law by taking one example : when we squeeze a filled balloon, the volume occupied by the air inside the balloon decreases. This is accompanied by an increase in the pressure exerted by the air on the balloon, as a consequence of Boyle’s law. As the balloon is squeezed further, the increasing pressure eventually pops it.

Note: There is one application of Boyle’s law where its understanding is beneficial. We understand this by taking an example of scuba diver. If a scuba diver rapidly comes back from a deep zone towards the surface of the water, the decrease in the pressure can cause the gas molecules in his/her body to expand. These gas bubbles can go on to cause damage to the diver’s organs and can also result in death.