Question

Which of the following is a Pythagorean triplet?
(a) 3, 4, 5
(b) 5, 12, 14
(c) 6, 8, 11
(d) 8, 5, 17

Answer 1

Hint: For solving this question we should know about the result of the Pythagoras Theorem in right-angled triangles. After that, we will examine every option separately and check whether it is a Pythagorean triplet or not.
Complete step-by-step answer:
Now, before we proceed just take a look at the result of the Pythagoras Theorem. The Pythagoras Theorem states that in a right-angled triangle as shown below $\Delta ABC$ , the square of the hypotenuse is equal to the sum of the squares of the other two sides.

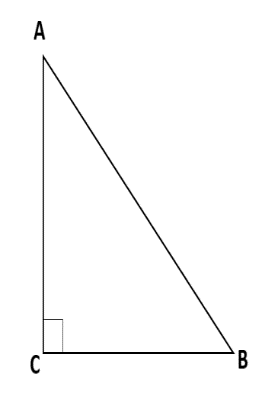
In the $\Delta ABC$ , $\angle ACB={{90}^{\circ}}$ and AB is the hypotenuse, BC is the base and AC is the perpendicular. From Pythagoras Theorem, we have:
$\begin{align}
  & {{\left( BC \right)}^{2}}+{{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}} \\
 & \Rightarrow {{a}^{2}}+{{b}^{2}}={{c}^{2}} \\
\end{align}$
Then, we can write, ${{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}={{\left( hypotenuse \right)}^{2}}$.
Now, we can easily understand the concept of the Pythagorean triplet.
Pythagorean Triplet: Pythagorean triplet are the values of hypotenuse, base and perpendicular which tend to represent a right-angled triangle. Integral solutions to the Pythagorean Theorem, ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$ are called Pythagorean triplet which contains three positive integers $a,b,c$ where $a < b < c$.
Now, we check all of the given options:
1) $3, 4, 5$ : In this case $3 < 4 < 5$ so, $a=3, b=4$ and $c=5$. Then,
$\begin{align}
  & {{a}^{2}}+{{b}^{2}}={{3}^{2}}+{{4}^{2}}=9+16=25 \\
 & {{c}^{2}}={{5}^{2}}=25 \\
 & \therefore LHS=RHS \\
\end{align}$
Thus, this is a Pythagorean triplet.
2) $5,12,14$ : In this case $5<12<14$ so, $a=5, b=12$ and $c=14$. Then,
$\begin{align}
  & {{a}^{2}}+{{b}^{2}}={{5}^{2}}+{{12}^{2}}=25+144=169 \\
 & {{c}^{2}}={{14}^{2}}=196 \\
 & \therefore LHS\ne RHS \\
\end{align}$
Thus, this is not a Pythagorean triplet.
3. $6,8,11$ : In this case as $6<8<11$ so, $a=6,b=8$ and $c=11$ . Then,
$\begin{align}
  & {{a}^{2}}+{{b}^{2}}={{6}^{2}}+{{8}^{2}}=36+64=100 \\
 & {{c}^{2}}={{11}^{2}}=121 \\
 & \therefore LHS\ne RHS \\
\end{align}$
Thus, this is not a Pythagorean triplet.
4. $8,5,17$ : In this case as $5<8<17$ so, $a=5,b=8$ and $c=17$ . Then,
$\begin{align}
  & {{a}^{2}}+{{b}^{2}}={{5}^{2}}+{{8}^{2}}=25+64=89 \\
 & {{c}^{2}}={{17}^{2}}=289 \\
 & \therefore LHS\ne RHS \\
\end{align}$
Thus, this is not a Pythagorean triplet.
Now, from the above results we conclude, that $3,4,5$ is a Pythagorean triplet.
Hence, (a) is the correct option.
Note: Here, we should know the result of Pythagoras Theorem correctly and its use to find the Pythagorean triplets. And we should avoid calculation mistakes while solving.