Question

Which of the following is not the net of a cube?
a)

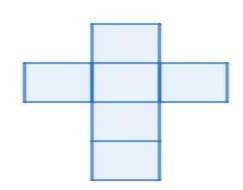
b)

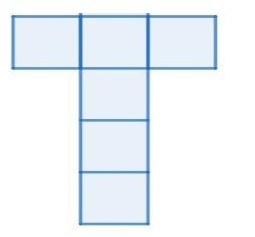
c)

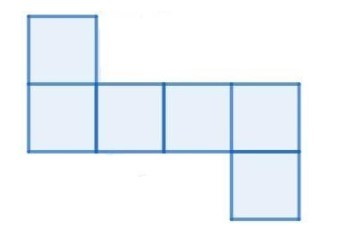
d)

Answer 1

Hint:We will fold the given net into a cube individually and check whether it is a cube or not. It is noted that cube net has always four boxes in consecutive as

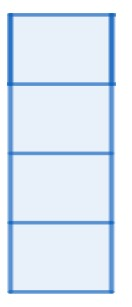
And the other two net can be replaced accordingly.

Complete step-by-step answer:
It is given in the question that we have to find the incorrect option among A,B,C,D that among them is not the net of a cube. So, basically a cube is a 3-dimensional geometrical shape having six equal faces. All the faces of the cube are in the shape of a square.
Now, we will open the cube into the net and find all the possible ways to open a cube into the net. It is noted that the cube net always has four boxes consecutively. So, the possible ways are
Possibility A:

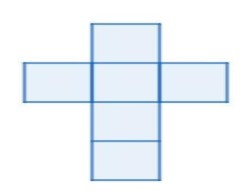
Possibility B:

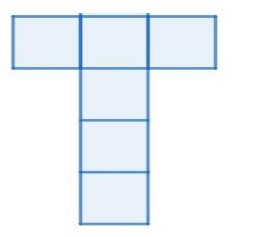
Possibility C:

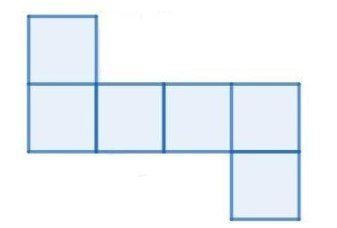
Therefore, only 3 ways possible by which we can open a cube into net form. Now, we will compare this obtained possibilities with all the given options individually.
Option a)

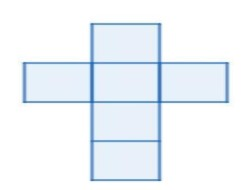
It is looking similar to our 1st possibility A, thus option a) is a net of cube.
Similarly option b)

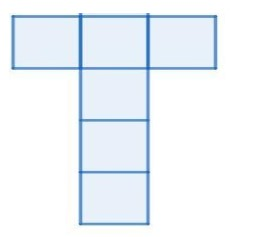
Is looking similar to our possibility B thus, option b) is a net of cube.
Also, option c)

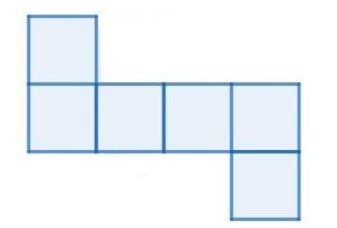
Is similar to possibility C thus option is also a net of cube.
Option d)

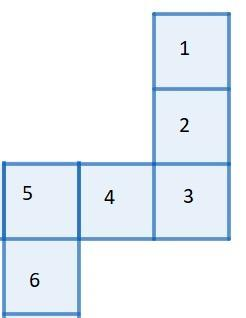
Has no match with our possibilities also when we fold the net then an overlapping will arise because of box 1 and box 6 which clearly show that option d) is not a net of a cube.

Note: Usually students confuse folding the cube and in confusion they may choose the wrong option. But, this type of question is totally based on our visualization. Only remember that we have six faces in a cube and for when we unfold the sides of cube we get 4 sides in a row consecutively as

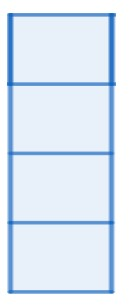
And two sides are arranged in all other possible ways. We can take our example of dice to relate our visualization. This will surely help us to solve such problems.