Question

Which of the following is paramagnetic with bond order\[0.5\]?
\[
  A.{F_2} \\
  B.{H_2}^ + \\
  C.{N_2} \\
  D.{\text{ }}{O_2}^ - \\
 \]

Answer 1

Hint: For solving this question, one should have a better understanding of how to draw the molecular orbital diagram as when you draw the diagram it becomes easy to solve this question. After drawing the diagram use the formula $B.O = \dfrac{{{{\text{N}}_{\text{B}}}{\text{ - }}{{\text{N}}_{\text{A}}}}}{2}$ to find out the bond order of each of the molecule.

Complete answer:
For solving this question we need to use the molecular orbital theory (MOT). This theory uses a method for describing the electronic structure of molecules using quantum mechanics. For drawing the molecular orbital diagram we need to know the electronic configuration of each of the following. for finding the bond order we use the formula :
$B.O = \dfrac{{{{\text{N}}_{\text{B}}}({\text{no}}{\text{. of electrons in bonding orbital) - }}{{\text{N}}_{\text{A}}}{\text{(no}}{\text{. of electrons in antibonding orbitals)}}}}{2}$
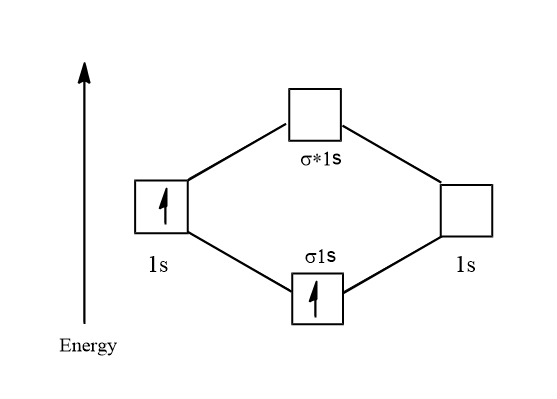
Electronic configuration of \[{F_2} = 1{s^2}2{s^2}2{p^5}\]
Its molecular orbital diagram will be:

As it can be seen in ${F_2}$ that there are no single electrons present in the any of the orbitals so it is diamagnetic and its bond order is:
$B.O = \dfrac{{{{\text{N}}_{\text{B}}}{\text{ - }}{{\text{N}}_{\text{A}}}}}{2}$
$ \Rightarrow \dfrac{{{\text{8 - 6}}}}{2}$
$ \Rightarrow \dfrac{{\text{2}}}{2} = 1$
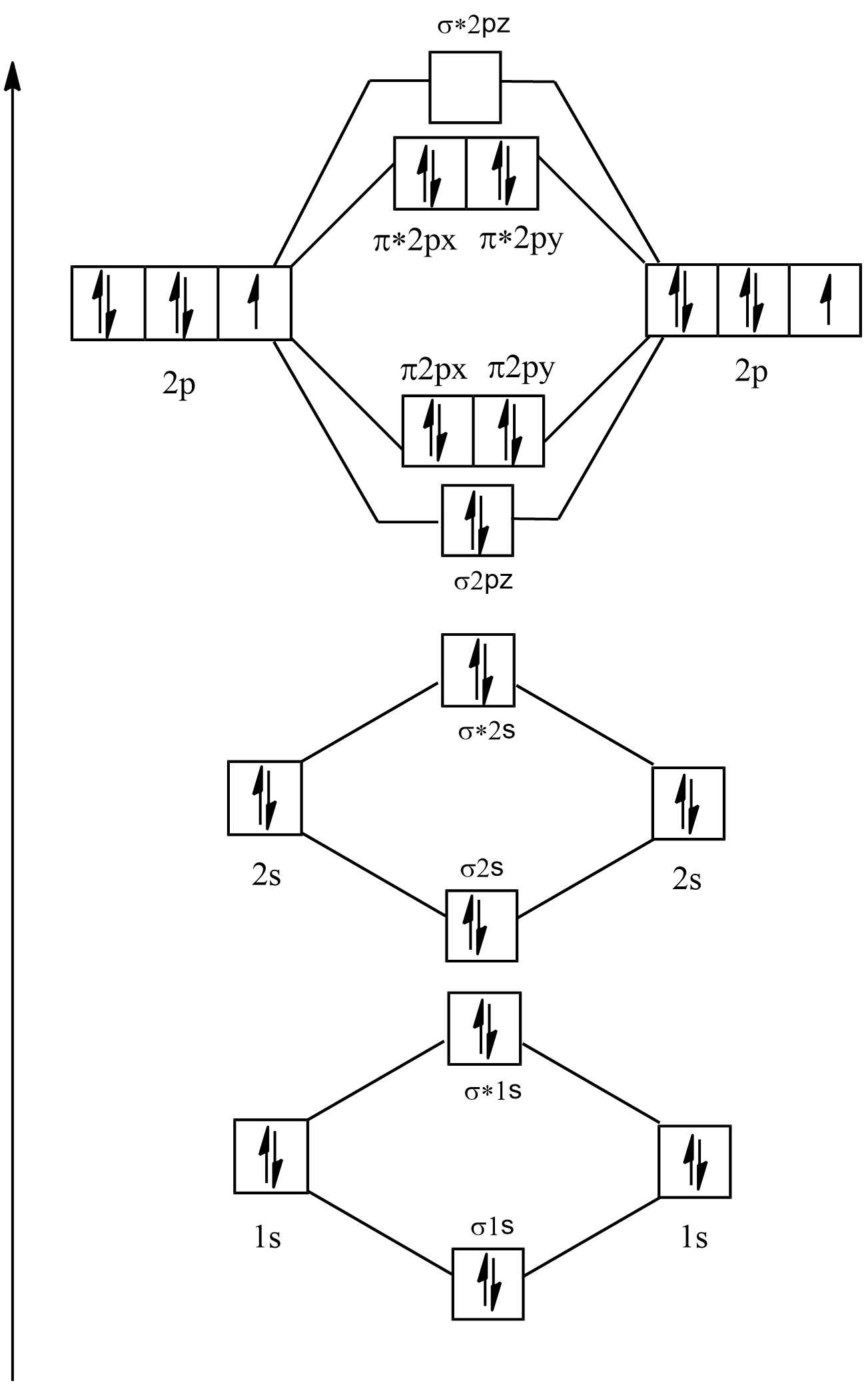
Electronic configuration of ${H_2}^ + = 1{s^1}$
Its molecular orbital diagram is:

$ \Rightarrow \dfrac{{\text{1}}}{2} = 0.5$
Thus there is one unpaired electron and so ${H_2}^ + $ is paramagnetic. Its bond order is:
$B.O = \dfrac{{{{\text{N}}_{\text{B}}}{\text{ - }}{{\text{N}}_{\text{A}}}}}{2}$
$ \Rightarrow \dfrac{{{\text{1 - 0}}}}{2}$

Electronic configuration of ${N_2} = 1{s^2}2{s^2}2{p^3}$
Molecular orbital diagram

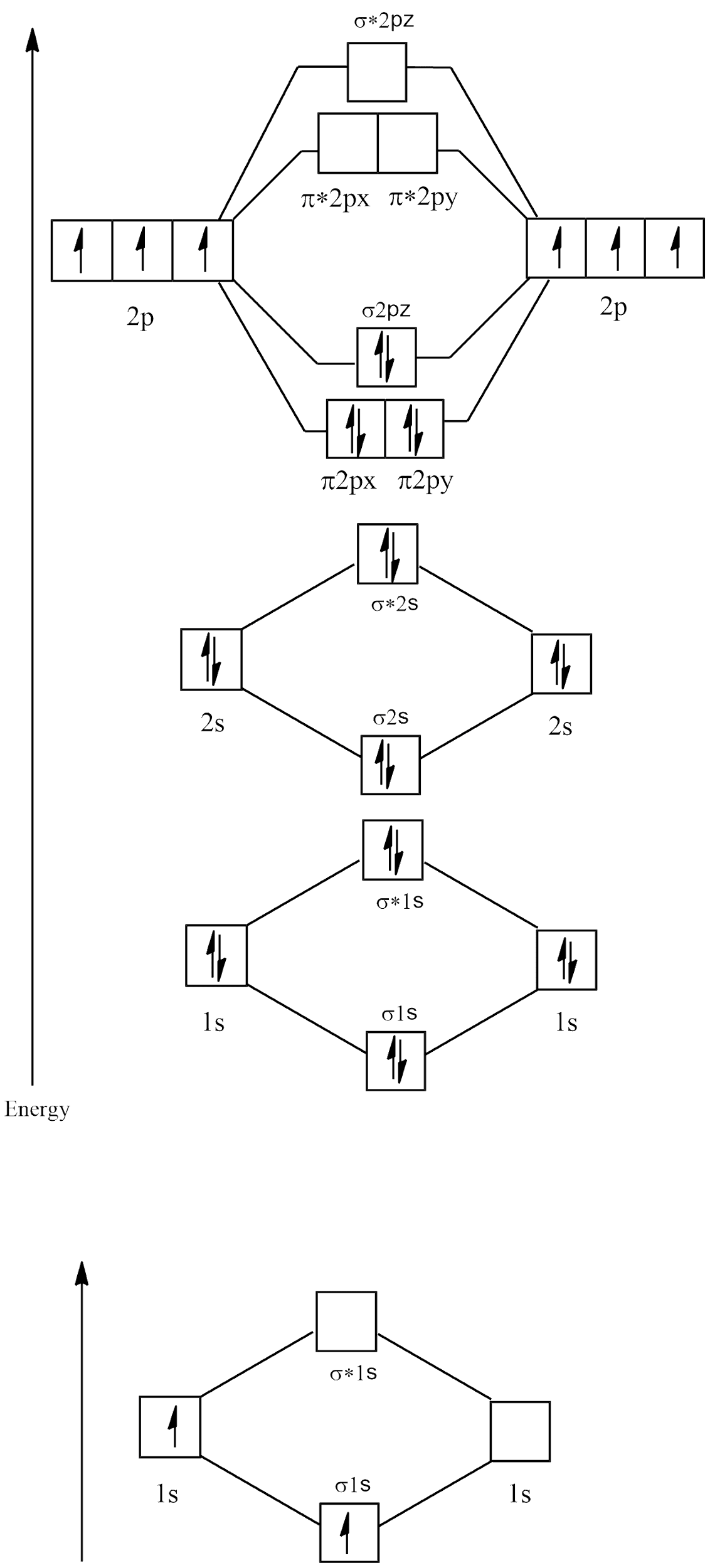
There are no unpaired electrons in ${N_2}$ and its bond order is:
$B.O = \dfrac{{{{\text{N}}_{\text{B}}}{\text{ - }}{{\text{N}}_{\text{A}}}}}{2}$
$ \Rightarrow \dfrac{{{\text{8 - 2}}}}{2}$
$ \Rightarrow \dfrac{6}{2} = 3$
Electronic configuration of ${O_2}^ - = 1{s^2}2{s^2}2{p^5}$
Molecular orbital diagram

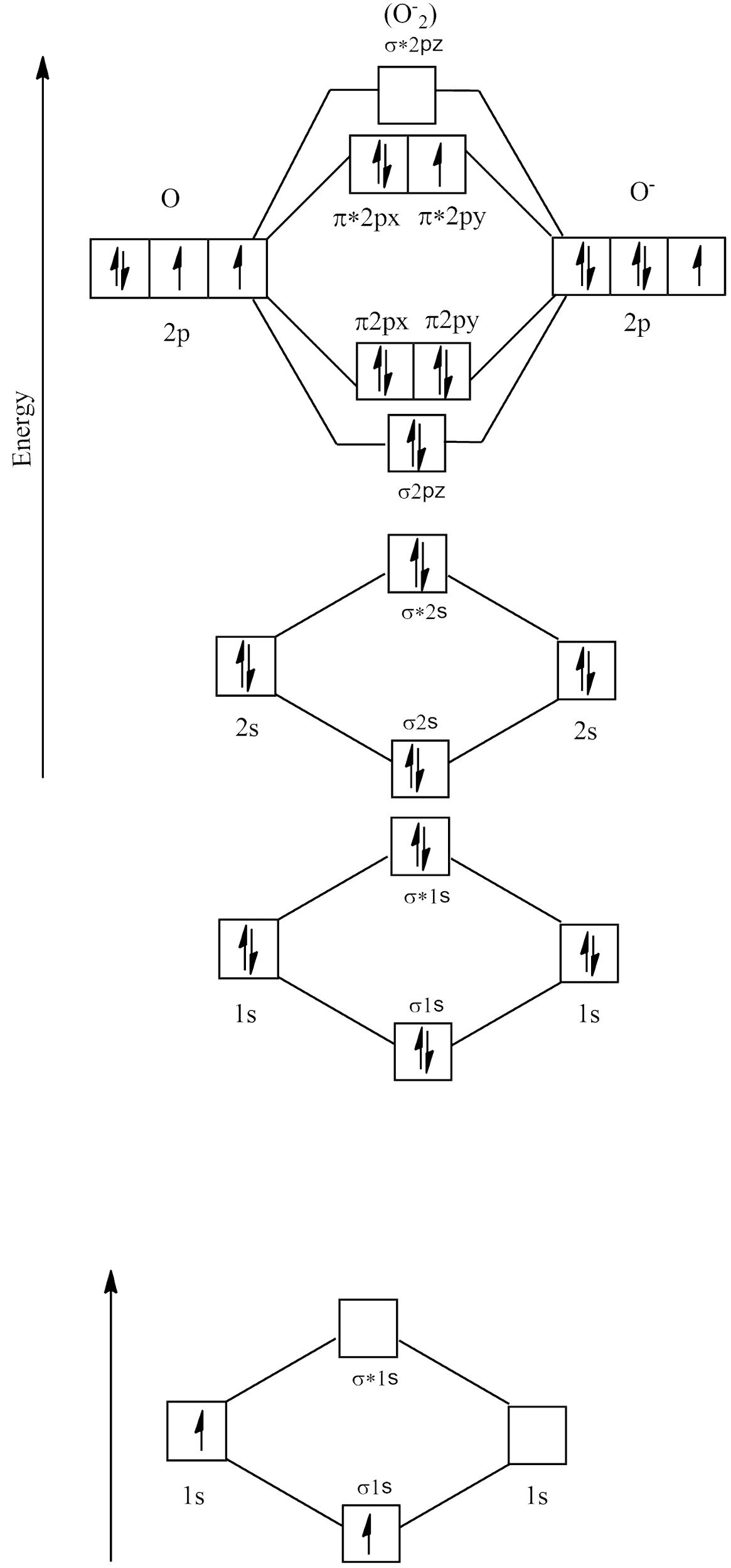
There are no unpaired electrons in ${O_2}^ - $ and its bond order is:
$B.O = \dfrac{{{{\text{N}}_{\text{B}}}{\text{ - }}{{\text{N}}_{\text{A}}}}}{2}$
$ \Rightarrow \dfrac{{{\text{8 - 5}}}}{2}$
\[ \Rightarrow \dfrac{3}{2} = 1.5\]
Thus, from the above data we can clearly see that only ${H_2}^ + $ is paramagnetic with the bond order of$0.5$.

Therefore the correct option is B. ${H_2}^ + $ .

Note:
While drawing the molecular orbital diagram for the elements above helium, the $1{s^2}$ orbital can be neglected because it always has $2$ electrons in it, and this orbital is always completely filled. A diatomic molecular orbital diagram is used to understand the bonding of a diatomic molecule. MO diagrams can be used to deduce the magnetic properties of a molecule and how they change with ionization.