Question

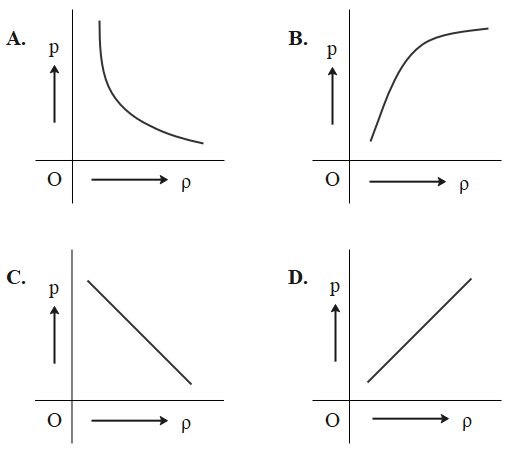
Which of the following shows the correct relationship between the pressure P and density of an ideal gas at constant temperature?

Answer 1

Hint: The relationship between the volume, pressure, temperature, and the amount of gas at any temperature for an ideal gas is given by the ideal gas equation. is our ideal gas equation. The density of a substance defined as its mass per unit volume Use these two definitions to deduce the relationship between the two asked quantities and then choose the appropriate graph.

Formula used:
$PV = nRT$, where ‘P’ is the pressure, ‘V’ is the volume, ‘n’ is the number of moles, ‘R’ is the universal gas constant and ‘T’ is the temperature.

Complete step by step answer:
The ideal relationship between the volume, pressure, temperature, and the amount of gas at any temperature is called the ideal gas equation.
$PV = nRT \cdots \cdots \cdots \left( 1 \right)$
in our ideal gas equation ‘P’ represents the pressure, ‘V’ represents the volume, ‘n’ represents the number of moles, ‘R’ represents the universal gas constant and ‘T’ is the temperature.
Rearranging equation (1), we have:
$P = \dfrac{{nRT}}{V}$
Let us multiply and divide the right-hand side of the equation by mass M of the substance.
$P = \dfrac{{MnRT}}{{MV}}$
But we know that the density of a substance, ${\text{ }}\rho = \dfrac{M}{V}$
So the above equation becomes:
$ \Rightarrow P = \dfrac{{\rho RT}}{M}$
That means the pressure is directly proportional to density since all others are constants at a constant temperature.
$P \propto \rho $
When we look into the graphs, only graph D supports our conclusion.
So, option D is the correct answer.

Note:
Gases behave ideally at a higher temperature and low pressure, as the intermolecular potential energy becomes less significant due to higher kinetic energy and the molecular size becomes less significant considering the void space between them. Use the ideal gas equation at a higher temperature and low-pressure conditions only or if it is specified that gas behaves ideally. In other conditions, they behave like real gases.