
How do write
Answer
466.5k+ views
Hint: We need to know the first ten prime numbers in the natural numbers. This question describes the operation of multiplication/ division. The final answer should involve only prime numbers. The definition of prime numbers is a number that is divided only by
Complete step by step solution:
In this question, we have to write
To solve the given question we would divide the
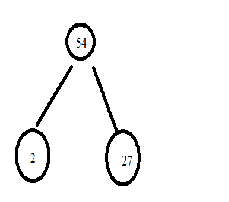
From the given prime numbers we can use
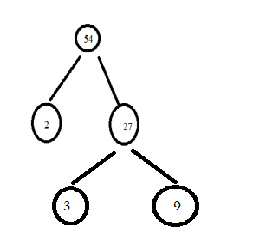
From the above step we cannot simplify
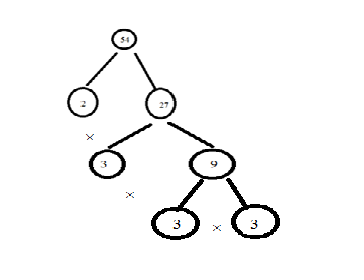
So, the final answer is, the product of prime factor for
(or)
Note: In this type of question we would use the operation of addition/ subtraction/ multiplication/ division. We need to know the first ten prime numbers. Note that
Complete step by step solution:
In this question, we have to write
To solve the given question we would divide the

From the given prime numbers we can use

From the above step we cannot simplify

So, the final answer is, the product of prime factor for
(or)
Note: In this type of question we would use the operation of addition/ subtraction/ multiplication/ division. We need to know the first ten prime numbers. Note that
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




