
Answer
419.4k+ views
Hint: To solve the given problem we should know the following properties of circle and straight line. The first thing we should know is the equation of the circle in center-radius form which is expressed as \[{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}\]. Here, \[\left( h,k \right)\] are the coordinates of the centre of the circle, and r is the radius of it. Next, we should know that the distance between two parallel tangents of a circle equals the diameter of the circle. We can find the value of radius by halving the diameter.
Complete step by step answer:
We are asked to write the equation of the circle with the given features. Let, the coordinates of the centre are \[\left( h,k \right)\] and the radius of the circle as r. using this, the centre-radius form of the circle can be expressed as \[{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}\].
As the lines \[y=-1\And y=9\] are both tangent to the circle. These two lines are also parallel to each other, we know that the distance between two parallel tangents equals diameter of the circle. The distance between these two lines is \[9-\left( -1 \right)=10\]. Using this property, we calculate the radius as \[\dfrac{10}{2}=5\].
If the bottom of the circle is at \[y=-1\] and the circle has a radius of 5, the y-coordinate of the centre of the circle must be \[-1+5=4\]. Also as the Y-axis is also tangent to the circle, it means that the magnitude of the X-coordinate must be equal to the radius, we get \[\left| h \right|=5\]. As the centre lies in second quadrant the X-coordinate must be negative \[h=-5\].
Now we have values of all variables. We can write the equation as \[{{\left( x+5 \right)}^{2}}+{{\left( y-4 \right)}^{2}}={{5}^{2}}\]
We can also plot the circle as follows:
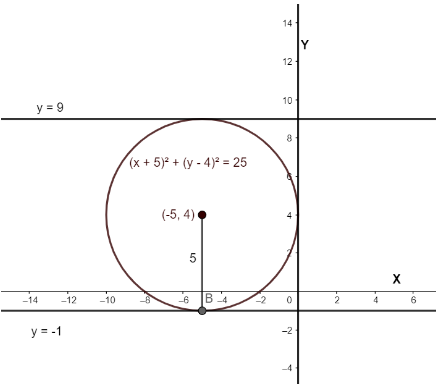
Note: To solve these types of questions, we should know the properties of circles and tangents of the circles. The distance between the two tangents is equal to the diameter of the circle. Calculation mistakes while solving these questions should be avoided.
Complete step by step answer:
We are asked to write the equation of the circle with the given features. Let, the coordinates of the centre are \[\left( h,k \right)\] and the radius of the circle as r. using this, the centre-radius form of the circle can be expressed as \[{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}\].
As the lines \[y=-1\And y=9\] are both tangent to the circle. These two lines are also parallel to each other, we know that the distance between two parallel tangents equals diameter of the circle. The distance between these two lines is \[9-\left( -1 \right)=10\]. Using this property, we calculate the radius as \[\dfrac{10}{2}=5\].
If the bottom of the circle is at \[y=-1\] and the circle has a radius of 5, the y-coordinate of the centre of the circle must be \[-1+5=4\]. Also as the Y-axis is also tangent to the circle, it means that the magnitude of the X-coordinate must be equal to the radius, we get \[\left| h \right|=5\]. As the centre lies in second quadrant the X-coordinate must be negative \[h=-5\].
Now we have values of all variables. We can write the equation as \[{{\left( x+5 \right)}^{2}}+{{\left( y-4 \right)}^{2}}={{5}^{2}}\]
We can also plot the circle as follows:

Note: To solve these types of questions, we should know the properties of circles and tangents of the circles. The distance between the two tangents is equal to the diameter of the circle. Calculation mistakes while solving these questions should be avoided.



