Question

Write an expression for the magnitude of resultant vector ‘R’ of two vectors ‘A’ and ‘B’ acting at a point. When will this resultant vector ‘R’ be maximum?

Answer 1

Hint: There are majorly two types of quantities, scalar and vector quantities. All the quantities are divided into these two categories. Scalar quantities are those quantities, which have only magnitude eg – mass, speed, pressure, etc. Vector quantities are those which have both magnitude and directions eg – weight, velocity and thrust.

Complete step-by-step answer:
Since we can’t directly add vectors like scalars, hence we have to find out some other way out.
Let two vectors A and B inclined at an angle ‘$\theta$’ at a point.

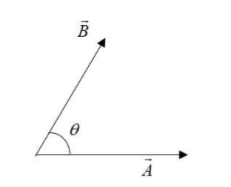
We know that a vector can be displaced anywhere in the space without altering the magnitude and direction. Thus using this property, we will displace the vector $\vec B$. Now let the magnitude of the resultant of both be $\vec R$ making an angle $\alpha$with the vector $\vec A$:

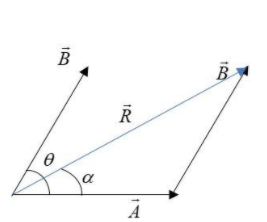
Now, the only thing we’ll do is that we’ll take the component of $\vec B$ along $\vec A$ and perpendicular to it.

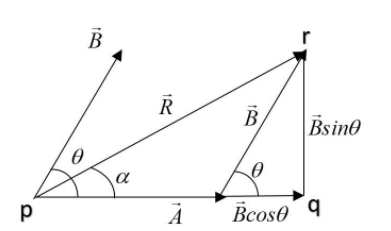
After dropping perpendicular from the head of $\vec R$, a right angled triangle (pqr) is formed.
Hence applying Pythagoras theorem in triangle (pqr), we get;
$(pr)^2 = (qr)^2+(pq)^2$
As $pq = \vec A + \vec Bcos\theta , \ qr = \vec B sin\theta \ and \ pr = \vec R$
Hence putting the values, we get:
$(\vec R)^2 = (\vec B sin \theta)^2+(\vec A + \vec B cos\theta)^2 = B^2 sin^2\theta + A^2 + B^2 cos^2 \theta +2 A B cos \theta$
Or $R^2 = B^2(sin^2 \theta + cos^2 \theta) + A^2 + 2AB cos\theta = A^2 + B^2 + 2AB cos\theta$ [$sin^2 \theta + cos^2 \theta = 1$]
Or $R = \sqrt{A^2+B^2+2ABcos\theta}$
Hence we get the resultant of two vectors as $R = \sqrt{A^2+B^2+2ABcos\theta}$. But this is only the magnitude.
For direction:
In triangle (pqr), $tan \alpha = \dfrac{\vec B sin \theta}{\vec B cos \theta + A}$
Or $\alpha =tan^{-1}{ \dfrac{\vec B sin \theta}{\vec B cos \theta + A}}$
Now, magnitude is maximum of $cos\theta$ is maximum = 1.
Putting it in $R = \sqrt{A^2+B^2+2ABcos\theta}$
$R = \sqrt{A^2+B^2+2AB} = \sqrt{(A+B)^2} = A+B$
Thus magnitude is maximum if the vectors are in the same direction.

Note: In the above expression, we have the magnitude $R = \sqrt{A^2+B^2+2ABcos\theta}$, which has nothing to do with the direction of $\vec R$ i.e. resultant whereas in expression, $\alpha =tan^{-1}{ \dfrac{\vec B sin \theta}{\vec B cos \theta + A}}$ we have nothing to do with the magnitude of $\vec R$.