Question

How do you write the equation of the circle with diameter endpoints of \[\left( 5,8 \right)\] and \[\left( 5,-4 \right)\] ?

Answer 1

Hint: The above given problem is a very simple problem of coordinate geometry. The sub-topic of the problem is circle, and for solving such problems we need to first understand what the different forms of circles are possible. The most generalised form of circle that we can represent, given that we have the centre of the circle and we its radius is \[{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}\] . Here in this equation, we have, \[\left( h,k \right)\] as the centre of the circle and ‘r’ as the length of the radius of the circle. However, to find the equation of the circle when the end points of the diameter is given, we first assume any point on the circle and apply the property that any diameter of a circle subtends a right angle at the circumference of the circle.

Complete step by step answer:
Now we start off with the solution to the given problem by writing that, the product of the slope of the two lines, one joining one given point and the arbitrary point on the circumference of the circle, and another joining the given point and the arbitrary point equals “ $-1$ ”. Let the arbitrary point be \[\left( x,y \right)\] . So the slope of the first line is,
\[{{m}_{1}}=\dfrac{y-8}{x-5}\] . The slope of the second line will be \[{{m}_{2}}=\dfrac{y+4}{x-5}\]
Now we can write that \[{{m}_{1}}\times {{m}_{2}}=-1\]
Evaluating this we get,
\[\begin{align}
  & {{m}_{1}}\times {{m}_{2}}=-1 \\
 & \Rightarrow \dfrac{y-8}{x-5}\times \dfrac{y+4}{x-5}=-1 \\
 & \Rightarrow \left( y-8 \right)\left( y+4 \right)=-{{\left( x-5 \right)}^{2}} \\
 & \Rightarrow {{y}^{2}}-8y+4y-32=-\left( {{x}^{2}}-10x+25 \right) \\
 & \Rightarrow {{y}^{2}}-4y-32=-{{x}^{2}}+10x-25 \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}-10x-4y-7=0 \\
\end{align}\]
So \[{{x}^{2}}+{{y}^{2}}-10x-4y-7=0\] is our final equation of the circle.

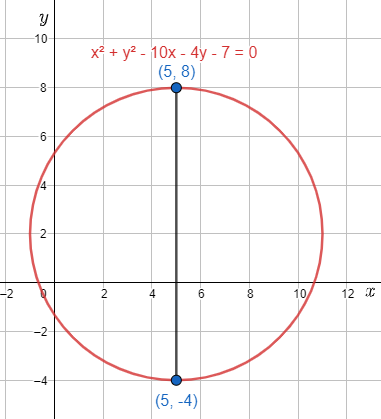
Note: For conic section problems the most important thing to solve the problems efficiently is to remember all possible equations and formulae of the topic. We need to remember concepts like, a diametrical chord subtends a right angle at the circumference of the circle. We apply the product of the slopes of two lines to ‘ $-1$ ’ and from this relation we can very easily find out the required equation of the circle.