Question

Write the formula for LSA of cuboid and explain each term in it.

Answer 1

Hint: Lateral surface area of the cuboid is given by, (the total surface area of the cuboid) – (area of the bottom surface + area of the top surface). We will find the lateral surface of the cuboid by adding the surface area of all the sides of the cuboid except the bottom and top of the cuboid.

Complete step-by-step solution -
It is given in the question that we have to find the formula for LSA of cuboid and explain each term in it.
We know that cuboid is a 3D solid shape with 6 faces. We can represent a cuboid of length ‘l’, height ‘h’ and breadth ‘b’ as follows.

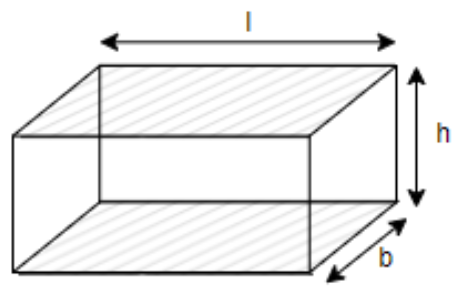
The lateral surface area of the cuboid can be found out by the addition of all the faces except the shaded faces in the above figure, as we do not consider the top and the bottom faces while finding the lateral surface area of a cuboid.
Now, if we open the cuboid, we can represent it as follows.

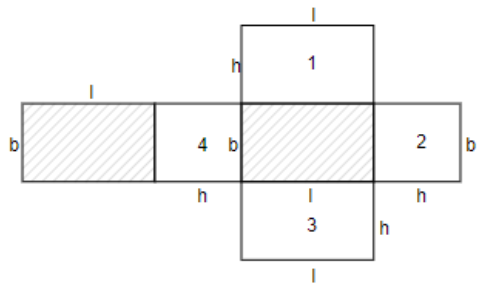
Now, in the above figure, the shaded boxes represent the top and the bottom surfaces of the cuboid which will not be considered in our calculation of the lateral surface area.
So, we have to take the sum of areas of the remaining boxes. Hence, the lateral surface area of the cuboid is given by,
Area of box 1 + Area of box 2 + Area of box 3 + Area of box 4
Now, we know that all the four unshaded boxes are rectangles and we know that the area of a rectangle is given by the product of its length and breadth. So, we can say,
Area of box 1 = $l\times h$
Area of box 2 = $b\times h$
Area of box 3 = $l\times h$
Area of box 4 = $b\times h$
Therefore, we can write the lateral surface area of the cuboid as,
\[\begin{align}
  & \left( l\times h \right)+\left( b\times h \right)+\left( l\times h \right)+\left( b\times h \right) \\
 & 2\left( l\times h \right)+2\left( b\times h \right) \\
\end{align}\]
On taking 2h as common from both the terms, we get,
$2h\left( l+b \right)$
Therefore, we get the lateral surface area of the cuboid as $2h\left( l+b \right)$.

Note: The possible mistake that the students can make in this question is by writing the lateral surface area of the cuboid as, (the total surface area of the cuboid) – (area of the bottom surface) and this is wrong and will result in the wrong answer. So, the students must remember that in the lateral surface area of a cuboid, the bottom and top faces are not considered.