Question

Write the number of the faces, edges and vertices of a tetrahedron.

Answer 1

Hint: To get the number of faces, edges and vertices of a tetrahedron, first of all draw a tetrahedron and understand what it is. It is basically in the shape of a triangular pyramid. Then try to name its vertices to find the numbers of faces, edges and vertices.

Complete step-by-step answer:
Here we have to find the number of faces, edges and vertices of a tetrahedron.
Before proceeding with this question, we must know what a tetrahedron is. In geometry, a tetrahedron which is also known as a triangular pyramid is a polyhedron composed of four triangular faces. It is a polyhedron with flat triangular base and triangular faces connecting the base to a common point. Tetrahedron is symmetrical, so in a tetrahedron, any of the four faces can be considered as the base of the tetrahedron.
Also, in a regular tetrahedron, all four faces are equilateral triangles. It is one of the five regular platonic solids which have been known since antiquity. In a regular tetrahedron, all faces are of the same size and shape, that is they are congruent and all the edges have equal length.
Diagrammatically, we can show tetrahedron in 3 dimension as follows:

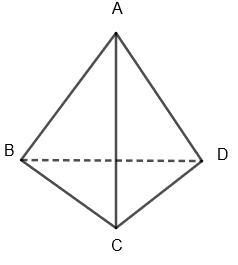
Here \[\Delta BCD\] is the base and \[\Delta \text{ABC},\Delta \text{ABD and }\Delta \text{ACD}\] are faces connecting base to vertex A.
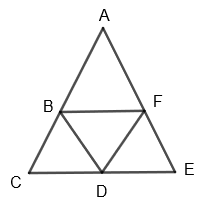
We can draw the net of tetrahedron as,

Now, to find the number of faces, edges and vertices of tetrahedron we will draw the image of tetrahedron in 2D as follows:

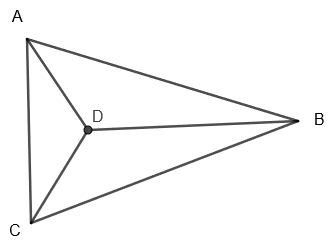
In the above figure, we can see that tetrahedron has a total four vertices and that are A, B, C and D.
Also, it has four triangular faces that are \[\Delta \text{ADC},\Delta \text{ABD,}\Delta \text{BDC and }\Delta \text{ABC}\].
Also, it has six edges that are AD, DC, AC, AB, DB and BC.
Hence, we have found that in tetrahedron,
Number of faces = 4
Number of edges = 6
Number of vertices = 4

Note: In geometry, we have a formula known as Euler’s formula. This is applicable for any polyhedron that doesn’t intersect itself. This says that, the number of faces plus the number of vertices minus the number of edges always equals 2. This can be written as: F + V – E = 2. We can also verify this formula for tetrahedron by substituting F = 4, V = 4 and E = 6, we get,
4 + 4 – 6 = 8 – 6 = 2
Hence, our answer is correct.