Question

Write the pair of vertically opposite angles.

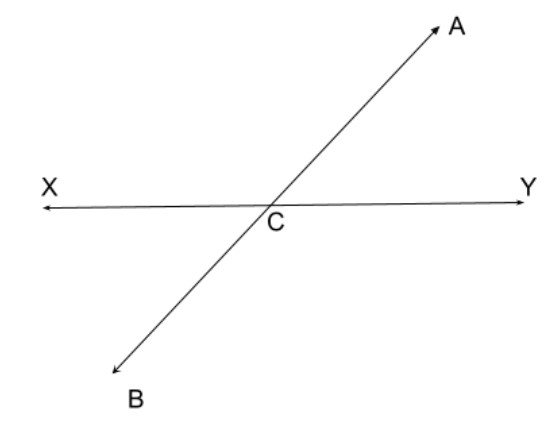
Answer 1

Hint:Vertical Angles are the angles opposite each other when two lines cross. "Vertical" in this case means they share the same Vertex (corner point).Using this definition we try to find vertical opposite angles from the figure.

Complete step-by-step answer:
The given image is,

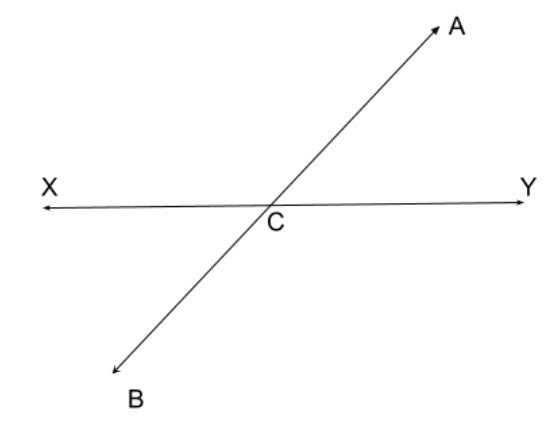
Vertical Angles are the angles opposite each other when two lines cross. "Vertical" in this case means they share the same Vertex (corner point).
Here \[AB\] and \[XY\] are two intersecting lines. They meet at \[C\].
Then the vertical angles are \[\angle ACY,{\text{ }}\angle XCB\,\&\, \angle XCA,{\text{ }}\angle BCY\]
The interesting thing here is that, vertical angles are equal.
So,
\[\angle ACY = \angle XCB\]
\[\angle XCA = \angle BCY\]

Thus we get, the pair of vertically opposite angles are \[\angle ACY,{\text{ }}\angle XCB\,\&\, \angle XCA,{\text{ }}\angle BCY\].

Note:When two lines intersect each other, then the opposite angles, formed due to intersection are called vertical angles or vertically opposite angles. A pair of vertically opposite angles are always equal to each other. Also, a vertical angle and its adjacent angle are supplementary angles, that is they add up to \[180^\circ \]. For example, if two lines intersect and make an angle, say \[X = 45^\circ \], then its opposite angle is also equal to \[45^\circ \]. And the angle adjacent to angle \[X\] will be equal to \[180^\circ - 45^\circ = 135^\circ \].
When two lines meet at a point in a plane, they are known as intersecting lines. When the lines do not meet at any point in a plane, they are called parallel lines.