Question

How do you write the polar equation r = 2 in rectangular form ?

Answer 1

Hint: In polar form we write the equation in the form of $\left( r,\theta \right)$ , where r is the distance of the point from origin and $\theta $ is the angle between positive X axis and line segment joining the point and origin. So we can write x as $r\cos \theta $ and y as $r\sin \theta $ , the value of r is $\sqrt{{{x}^{2}}+{{y}^{2}}}$ and the value of $\tan \theta $ is equal to $\dfrac{y}{x}$ .

Complete step by step answer:
The polar equation given in the question is r = 2
We have to write the above equation in rectangular form. The graph of the equation is a collection of all points which are at a distance of 2 units from the origin , so it is a circle with a center at origin.
We know in polar form the value of r is equal to $\sqrt{{{x}^{2}}+{{y}^{2}}}$ , to convert the equation into rectangular form we can replace r with $\sqrt{{{x}^{2}}+{{y}^{2}}}$
So the rectangular form of the equation is $\sqrt{{{x}^{2}}+{{y}^{2}}}=2$
Squaring both sides we get ${{x}^{2}}+{{y}^{2}}=4$
The equation ${{x}^{2}}+{{y}^{2}}=4$ is a circle with center at origin and with radius equals 2 units we can draw the graph.

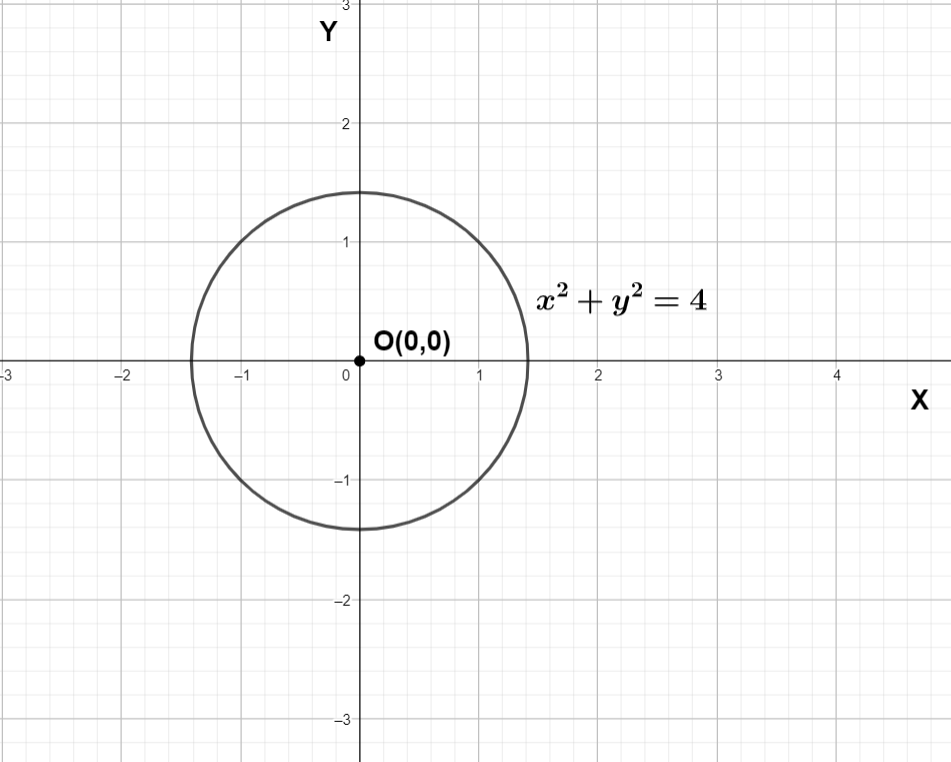
We can see the graph of r = 2 or ${{x}^{2}}+{{y}^{2}}=4$ is a circle with center at origin and radius equals to 2.

Note: When we write an equation in polar form we know that we can write x as $r\cos \theta $ and y as $r\sin \theta $ but keep in mind that while writing the value of $\theta $ don’t write $\theta $ is equal to ${{\tan }^{-1}}\dfrac{y}{x}$
Here is the thing $\tan \theta $ is equal to $\dfrac{y}{x}$ , but $\theta $ is not equal to ${{\tan }^{-1}}\dfrac{y}{x}$ because the range of ${{\tan }^{-1}}\dfrac{y}{x}$ is from $-\dfrac{\pi }{2}$ to $\dfrac{\pi }{2}$ but the value $\theta $ can be greater than $\dfrac{\pi }{2}$ .