Question

Write the process of finding the unknown resistance by meter bridge and deduce the necessary mathematical formula.

Answer 1

Hint: In this question we have been asked to describe the process of finding the unknown resistance by meter bridge. Therefore, to solve this question, we shall discuss what is a meter bridge. We shall also briefly discuss the construction and working using a labelled diagram. We know that a meter bridge is an instrument that works on the principle of a wheatstone bridge. Therefore, using this we shall deduce a suitable mathematical formula.

Complete step by step answer:
Meter bridge also known as slide wire bridge is an instrument working on the principle of wheatstone bridge. The construction of a meter bridge is as shown in the figure below. It usually consists of a metre long wire of uniform cross section area. A source of emf is connected across AC. The resistance box R is attached between two copper strips another copper strips contain the unknown resistance S. A movable jockey and galvanometer are connected at B as shown.

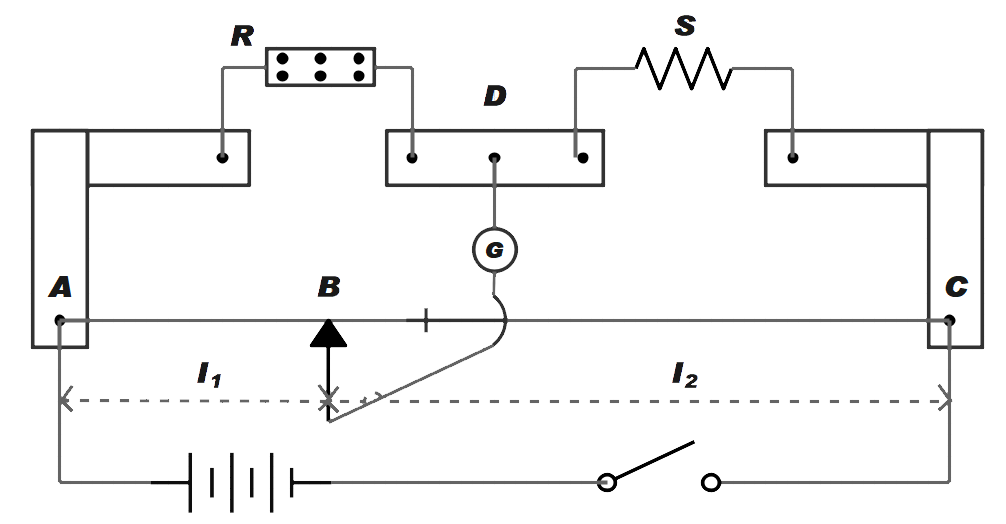
Working: After taking the suitable resistance R from the resistance box, we touch the wire at A and C to observe opposite deflection. By moving the jockey and changing the known resistance, a stable condition of wheatstone bridge is obtained.
Now, if P and Q are the parts of wire AC,
Then the balanced condition of the bridge can be given by,
\[\dfrac{P}{Q}=\dfrac{R}{S}\] ……………….. (1)
If the resistance of unit length of wire is and the balance point occurs at L cm rom A then BC = (100-L) cm
Let, P be the resistance of wire at AB and Q be the resistance of wire of part BC
So,
\[P=\sigma L\] ……………. (2)
Similarly,
\[Q=\sigma (100-L)\] …………….. (3)
Now, from (1), (2) and (3)
We get,
\[\dfrac{R}{S}=\dfrac{\sigma L}{\sigma (100-L)}\]
On solving,
\[S=\dfrac{(100-L)R}{L}\]
Now, we know that
\[S=\rho \dfrac{l'}{A}\]
Where l’ is the length of unknown resistance and \[A=\pi {{r}^{2}}\]
Therefore, after substitution
We get,
\[l'=\rho \dfrac{(100-L)\times \pi {{r}^{2}}}{L}\]

Note:
The resistance by the copper strips is neglected while calculating the unknown resistance. Therefore, the chances of calculation error is high. The resistance of end points also affects the sensitivity of the metre bridge. A Carey Foster bridge is used to overcome this effect. If the current flows for a long time in the wire, the wire will heat up and the resistance is varied. The jockey should not slide tightly, this increases the resistance and changes the value of unknown resistance.