Question

Write the relation between the angular momentum and torque. What is the torque acting on a body rotating with constant angular momentum?

Answer 1

Hint: We need to understand the physical quantities angular momentum and torque to understand the relation existing between them. We can find the definition for the angular momentum and the torque and easily solve the given problem.

Complete answer:
The angular momentum is the rotational analogue of the linear momentum and the torque is the rotational analogue of the force. The angular momentum is defined as the momentum imparted on a rotating object due to its perpendicular distance from the center of rotation. It is given as the cross product of the radius or the distance from the center of rotation to the center of mass of the object and the linear momentum.
i.e.,
\[\begin{align}
  & \overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p} \\
 & \therefore \overrightarrow{L}=\left| \overrightarrow{r} \right|\left| \overrightarrow{p} \right|\sin \theta \widehat{n} \\
\end{align}\]
Where, L is the angular momentum,
r is the distance from the center of mass to the axis of rotation,
p is the linear momentum,
\[\theta \]is the angle between ‘r’ and ‘p’,
\[\widehat{n}\] is the direction of the angular momentum.
                            

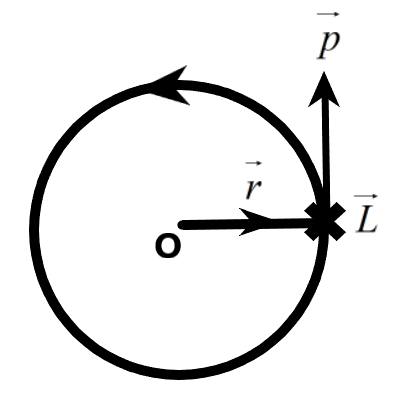
The torque on a rotating body is the force acting perpendicular to the distance between the axis of rotation. It provides the angular acceleration necessary for the object to undergo rotational motion. The torque is defined as the rate of change of angular momentum which is the same as the cross product of the linear force and the distance from the axis.
i.e.,
\[\begin{align}
  & \overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F} \\
 & \Rightarrow \overrightarrow{\tau }=\left| \overrightarrow{r} \right|\left| \overrightarrow{F} \right|\sin \theta \widehat{n} \\
 & \text{and,} \\
 & \overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p} \\
 & \Rightarrow \dfrac{d\overrightarrow{L}}{dt}=\dfrac{d(\overrightarrow{r}\times \overrightarrow{p})}{dt} \\
 & \therefore \overrightarrow{\tau }=\dfrac{d\overrightarrow{L}}{dt}=\left| \overrightarrow{r} \right|\left| \overrightarrow{F} \right|\sin \theta \widehat{n} \\
\end{align}\]
So, the torque is the rate of change of angular momentum. We are given that the angular momentum is constant for a situation. In such a situation the torque will be zero.
i.e.,
\[\begin{align}
  & \overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p}=\text{constant} \\
 & \therefore \overrightarrow{\tau }=\dfrac{d\overrightarrow{L}}{dt}=0 \\
\end{align}\]
The torque will be zero in such a case. This is the required solution.

Note:
We can see that the force and the angular momentum are the same quantities as far as the rotational motion is concerned. But the net force acting on the system will not be equal to the angular momentum and therefore they are treated as different entities.