Revision Notes for Class 11 Chemistry Chapter 2- Structure of Atom

VALENCY OF SOME COMMON BASIC AND ACIDIC RADICALS

Electrovalent Positive Ions (Basic Radicals)

ELECTROVALENT NEGATIVE IONS (ACIDIC RADICALS)

1. INTRODUCTION

This chapter delves into the mysterious and surprising world of atoms on the inside. Atoms and their structures underpin all of chemistry. We'll also look at how electrons behave and the repercussions of their actions.

1.1 Discovery of fundamental particles

Dalton's atomic theory was successful in explaining the laws of conservation of mass, constant composition, and multiple proportion, but it failed to explain the results of numerous tests, such as the fact that solids like glass or ebonite create electricity when touched with silk or fur.

1.1.1 Electron discovery Of 1879, William Crookes investigated the electrical discharge in cathode ray discharge tubes, which are partially evacuated tubes. A discharge tube is a glass tube that is roughly 60cm long and has two thin metal bits called electrodes that are sealed inside. Crooke's tube is the name for this type of tube. The negative electrode is referred to as the cathode, whereas the positive electrode is referred to as the anode.

Invisible rays emanating from the cathode and producing a greenish light behind the perforated anode on the glass wall coated with phosphorescent substance ZnS are detected when a gas is confined at low pressure (10-4 atm) in a discharge tube is subjected to a high voltage (10,000V).

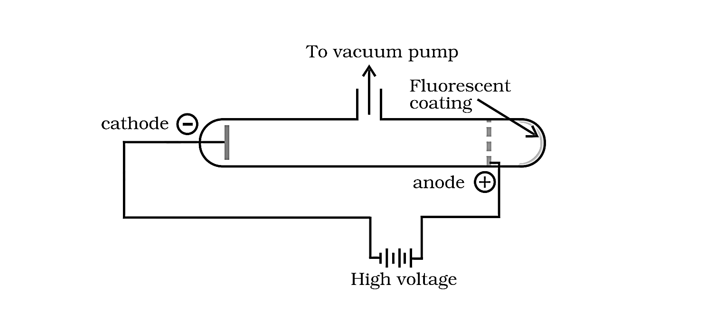
Cathode Ray Experiment

Cathode rays were the name given to these beams.

1.1.2 Characteristics

1. They cast a sharp shadow on solid objects in their route, implying that they are travelling in a straight line.

2. They are negatively charged because they are redirected towards the positive plate in an electric field. Stoney gave them the name electrons.

3. They can make a light paddle wheel that rotates in front of them. They have kinetic energy and are material particles, which means they have kinetic energy.

4. Their charge-to-mass ratio is 1.75882 1011C/kg.

5. They ionise the gases they pass through.

6. When they collide with a metallic target, they emit X-rays.

7. The material of the electrodes and the nature of the gas present in the cathode ray tube have no effect on the characteristics of cathode rays (electrons).

As a result, we can conclude that electrons are the fundamental building blocks of all matter.

1.1.3 Charge to mass ratio of electron

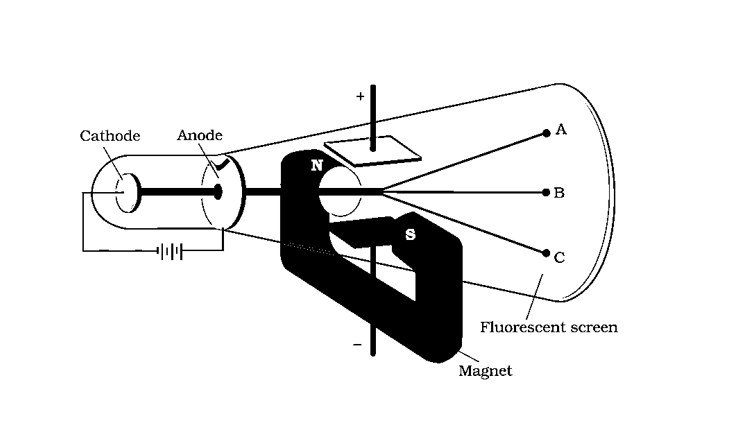
J.J. Thomson Experiment-Charge to Mass Ratio of Electron

J.J. Thomson used a cathode ray tube to measure the e/m ratio of electrons in 1897, employing electric and magnetic fields that were perpendicular to each other and to the path of electrons.

In the presence of an electric or magnetic field, the extent to which electrons deviate from their path is determined by: 

(a) the charge on the electron,

(b) the mass of the particle, and 

(c) the strength of the electric or magnetic field.

The electrons are deflected to point A when merely an electric field is applied. Electrons are deflected to point C when merely a magnetic field is provided. The electrons can hit the screen at point B by balancing the intensities of electric and magnetic fields.

1.1.4 Charge on the electron

To establish the charge on the electrons, R.A Millikan invented the oil drop experiment.

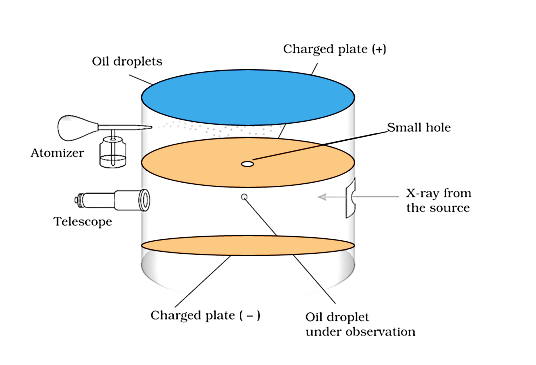
Millikan Invented the Oil Drop Experiment

Oil droplets in the form of mist were permitted to enter through a tiny hole in the upper plate of the electrical condenser in this manner. Through a microscope with a micrometre eye piece, the downward motion of these droplets was observed. Millikan was able to determine the mass of oil droplets by monitoring the velocity at which they fell. By passing an X-ray beam through the air inside the chamber, it was ionised. Collisions with gaseous ions gave these oil droplets their electrical charge.

Depending on the charge on the droplets and the polarity and strength of the voltage given to the plate, the fall of these charged oil droplets can be slowed, accelerated, or made immobile. Millikan discovered that the magnitude of electrical charge, q, on oil droplets is always an integral multiple of the electrical charge, e, by carefully monitoring the effects of electrical field intensity on the motion of oil droplets, q = n e, where n = 1, 2, 3…

The electron's charge is measured to be –1.6022 10–19C.

As a result, the mass of an electron was computed as

\[{\text{m = }}\dfrac{{\text{e}}}{{{\text{e/m}}}} = \dfrac{{1.6022 \times {{10}^{ - 19}}{\text{C}}}}{{1.758820{\text{ }}{{10}^{11}}{\text{C/ kg}}}} = 9.1094{\text{ }}{10^{ - 31}}{\text{ kg}}\]

1.1.5 Where do cathode rays come from?

Because the gas molecules are bombarded by the high-speed electrons discharged initially from the cathode, cathode rays are produced first from the cathode material and subsequently from the gas inside the discharge tube.

1.2.1 Proton discovery

Because the atom is electrically neutral as a whole and the presence of negatively charged particles has been proved, it was assumed that some positively charged particles must also be present. As a result, during his research with cathode rays, physicist Goldstein devised a unique discharge tube. Canal rays are a new type of ray that he found.

Canal rays get their name from the fact that they move in the opposite direction of cathode rays in a vacuum tube, passing through and emerging from a canal or hole in the cathode.

Anode rays are another name for them.

1.2.2 Properties:

They travel in straight lines for the most part.

2. They have a positive charge on them.

3. They are formed up of particles of substance.

4. The charge on the particles that make up anode rays is discovered to be dependent on the type of gas used.

5. It is discovered that the mass of the particles that make up anode rays is affected by the type of gas used.

6. The particle's charge to mass ratio (e/m) is discovered to be dependent on the gas used.

7. Their behaviour in electric and magnetic fields is diametrically opposed to that of electrons.

1.2.3 Origin of anode rays: Anode rays are thought to be created when high-speed electrons from cathode rays strike gaseous atoms, knocking away their electrons. These anode rays are formed in the space between the anode and the cathode and are not released by the anode.

When hydrogen was used as the discharge gas, the lightest charged particles were obtained. These particles have the highest e/m value. They had the smallest mass and a single positive charge. A proton was the name given to the particle.

A proton's charge is \[ + 1.6022 \times {10^{ - 19}}{\text{C}}\]

Mass of a proton = \[{\text{1}}{\text{.672}} \times {10^{ - 27}}{\text{kg}}\]

1.3.1 Neutron discovery

Rutherford proposed the theoretical requirement for the existence of a neutron particle in the atomic nucleus in 1920.

It was postulated that it be a neutral particle with a mass nearly equivalent to that of a proton. It was given the name neutron by him. Chadwick established its existence in 1932. When a beam of particles 2 4 (He) collided with Beryllium (Be), he saw that a new sort of particle was ejected. It was virtually the same mass as a proton (1.674 10–27kg) and had no charge.

\[\begin{gathered} {}_5^{11}{\text{B + }}{}_2^4{\text{He}} \to {}_7^{14}{\text{N + }}{}_0^1{\text{n}} \hfill \\ {}_4^9{\text{Be + }}{}_2^4{\text{He}} \to {}_6^{12}{\text{C + }}{}_0^1{\text{n}} \hfill \\ \end{gathered} \]

ATOMIC BUILDING BLOCKS

2. DEFINITIONS

2.1 Electron

A basic particle with a mass almost equivalent to 1/1837th of that of a hydrogen atom and one unit negative charge.

2.2 Proton

A basic particle with a mass almost equal to that of a hydrogen atom and one unit positive charge.

2.3 Neutron

A fundamental particle with a mass almost equal to that of a hydrogen atom but no charge.

3. MODEL THOMSON

Sir J. J. Thomson, the inventor of the electron, was the first to propose an atomic structure model.

(I) Electrons are found in every atom.

(ii) The entire atom is neutral. The total positive and negative charges must be the same.

He saw the atom's positive charge being evenly distributed around an atomic-sized sphere (about 10–10 m in diameter). The electrons were tiny particles with a negative charge equal to the positive charge in the atom when they were grouped together. They were like plums in a dessert, embedded in the atom. The charge distribution was such that the arrangement was the most stable. The plum - pudding model of the atom was popular at the time. Also available are the raisin pudding and watermelon models.

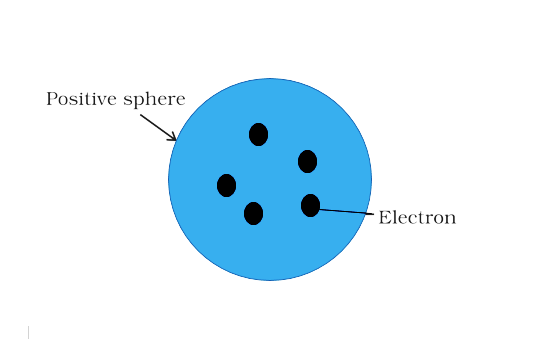
Plum - Pudding Model of the Atom

3.1 Drawbacks

Though the model was able to explain the atom's overall neutrality, it was unable to explain Rutherford's scattering experiments satisfactorily.

4. RUTHERFORD’S α-SCATTERING EXPERIMENT

In 1909, Rutherford conducted particle scattering experiments. A fine stream of alpha particles bombards an extremely thin gold foil (0.004nm) in this experiment. Behind the gold foil is a fluorescent screen (ZnS), on which points emerging from-particles were captured.

Polonium was employed as the -particles' source.

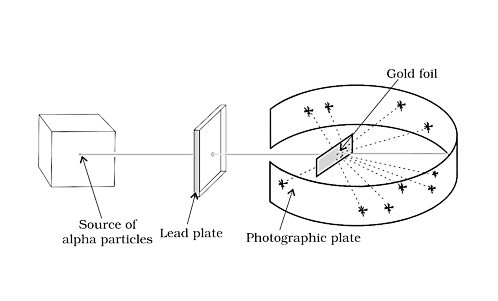
Rutherford’s α-Scattering Experiment

4.1 Observations

Rutherford conducted a series of tests utilising particle scattering by an extremely thin gold foil.

The following observations were made: 

(i) The majority of the particles (99 percent) pass through it without deflection or deviation.

(ii) Particles were deflected at tiny angles in several cases.

(iii) Only a few particles were deflected by considerable angles, and one particle was deflected by 180o on rare occasions.

4.2 Conclusions

(i) Because most particles flowed through it without deflection, an atom must be exceedingly hollow and made up mostly of empty space.

(ii) Only a few particles were deflected significantly. This means that: (a) Electrons cannot deflect heavy and positively charged particles due to their negative charge and low mass.

(b) There must be an extremely hefty and positively charged body in the atom, such as the nucleus, that prevents positively charged particles from passing through.

(c) Because the number of particles that experience 180o deflection is so small, the volume of a positively charged body must be a very small proportion of the atom's overall volume. This positively charged substance must be at the nucleus, which is the centre of the atom.

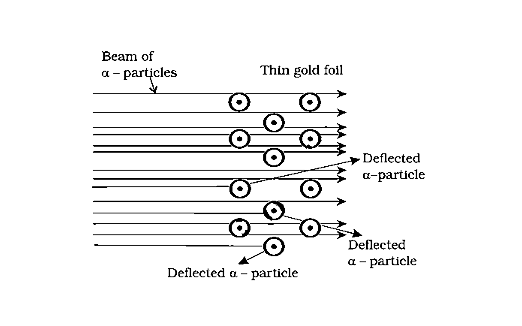
Scattering of  α-Particles

The radius of an atom is found to be in the range of 10–10m, while the radius of the nucleus is in the range of 10–15m. If a cricket ball represents a nucleus, the radius of an atom is around 5 kilometers.

4.3 Rutherford’s nuclear atomic model

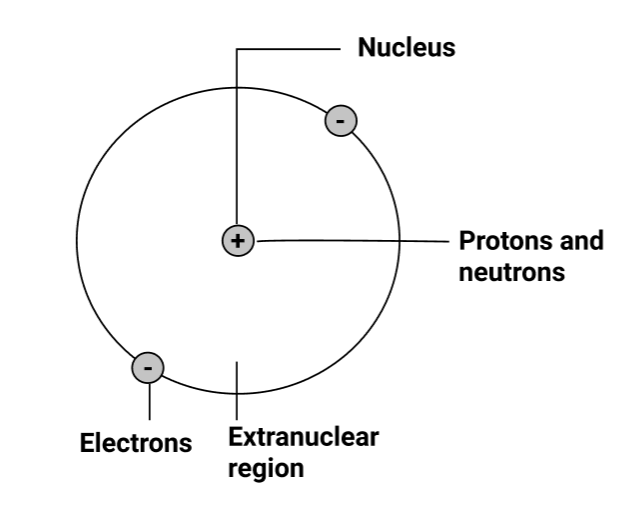
Rutherford’s Nuclear Atomic Model

(i) At the centre of an atom lies a tiny positively charged nucleus, which is surrounded by a hollow region known as the extra nuclear part.

(ii) Nucleons, which are made up of protons and neutrons, give the nucleus its positive charge, whereas electrons, which are found in the extra nuclear region, have minimal mass, and carry a negative charge.

(iii) Because the number of electrons in the atom equals the number of protons, it is electrically neutral. As a result, the nucleus' total positive charge is balanced by the electrons' total negative charge.

(iv) In the extranuclear section, electrons orbit the nucleus in circular routes known as orbits. As a result, an atom mimics the solar system, with the sun acting as the nucleus and the planets acting as circling electrons, and the model is referred to as the planetary model.

(v) The electrostatic force of attraction holds electrons and nuclei together.

(vi) Centrifugal forces perfectly balance the forces of attraction acting on the electron.

4.4 Drawbacks

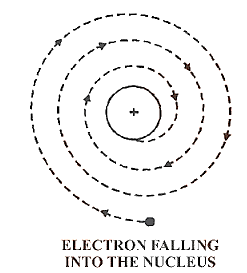
Drawbacks of Rutherford’s Nuclear Atomic Model

(i)Any charged entity in motion under the influence of attractive forces should radiate energy continually, according to classical mechanics. If this is the case, the electron will spiral and eventually fall into the nucleus, causing the structure to collapse. This type of behaviour is never seen.

(ii) It contains no information on the electronic structure of atoms, such as how electrons are dispersed around the nucleus and their energies.

5. ATOMIC NUMBER AND MASS NUMBER

5.1 Atomic number (Z)

The number of unit positive charges or protons contained in the nucleus of an element's atom is equal to the element's atomic number. It also represents the neutral atom's number of electrons. For example, the number of protons in Na is 11, hence the atomic number of Na is 11.

5.2 Mass number (A)

The nucleons are the elementary particles (protons and neutrons) that make up the nucleus of an atom.

An atom's mass number (A) is equal to the total of its protons and neutrons. It's always a number that's a whole number. As a result, the mass number (A) equals the sum of the number of protons (Z) and the number of neutrons (N)

Therefore, number of neutrons (n) = Mass Number (A) – Number of protons (Z) n = A – Z

The general notation that is used to represent the mass number and atomic number of a given atoms is $_Z^AX$

Where, ${\text{X}} - $ symbol of element

A - Mass number

$Z - $ atomic number

5.3 Isotopes, Isobars, isotones and Isoelectronic

5.3.1 Isotopes: Isotopes are same atomic number but differing mass number atoms of the same element. The discrepancy is due to the number of neutrons present.

The number of electrons in an atom determines its chemical characteristics. As a result, isotopes of the same element have the same chemical behaviour.

Isotopes of Hydrogen

Isotopes of Oxygen

Isotopes of Some Common Elements

5.3.2 Relative Abundance: In nature, varying percentages of an element's isotopes occur, which is referred to as relative abundance.

The average atomic mass of the element can be estimated using this relative abundance. Cl, for example, has an average atomic mass of 35.5 due to the presence of two isotopes, 35Cl and 37Cl, which are found in 75 percent and 25% abundance, respectively.

5.3.3 Isobars: Isobars are atoms of various elements with distinct atomic numbers but the same mass numbers.

5.3.4 Isotones: Isotones are atoms of various elements that have the same number of neutrons.

5.3.5 Isoelectronic: This term refers to species (atoms or ions) that have the same number of electrons. For example, \[{{\text{O}}^{\text{2}}}^{\text{--}}{\text{, }}{{\text{F}}^{\text{--}}}{\text{ , N}}{{\text{a}}^{\text{ + }}}{\text{ , M}}{{\text{g}}^{{\text{ + 2}}}}{\text{, A}}{{\text{l}}^{{\text{ + 3}}}}{\text{, Ne}}\], and so on.

To go deeper into the atomic secrets, we'll need to learn about electromagnetic radiations and Maxwell's Electromagnetic Wave Theory."

The first thorough description of the interaction between charged things and the behaviour of electric and magnetic fields was given by James Maxwell.

To go deeper into the atomic secrets, we'll need to learn about electromagnetic radiations and Maxwell's Electromagnetic Wave Theory."

The first thorough description of the interaction between charged things and the behaviour of electric and magnetic fields was given by James Maxwell.

6. ELECTROMAGNETIC RADIATIONS

Waves created by oscillating magnetic and electric fields that are perpendicular to each other and both perpendicular to the direction of motion are known as electromagnetic radiation.

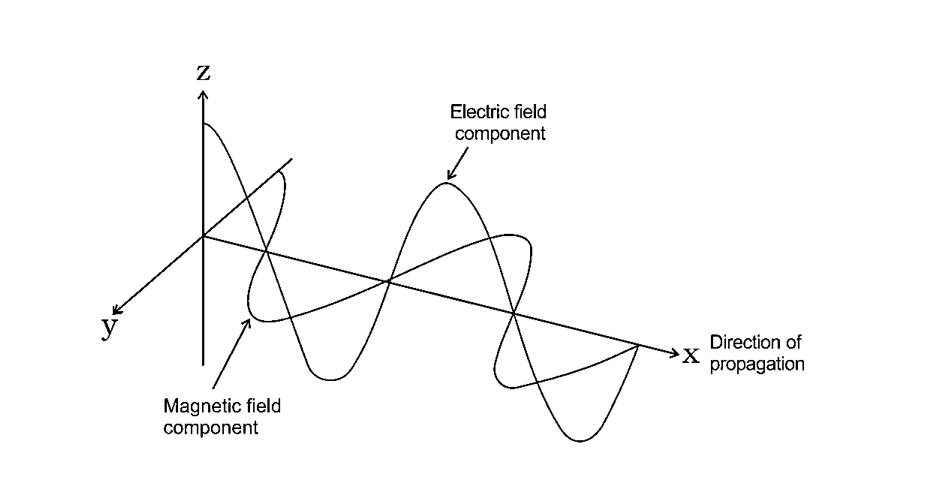
Electromagnetic Wave Graph

They do not require any medium and, unlike sound waves, can move in a vacuum.

Light is a type of radiation with wave properties.

The following are some of the characteristics of a wave:

1) Amplitude: The height of a wave's crest or trough (depth). metre (metric) (m)

2) Frequency: The number of waves that travel through a certain place in a second. Hertz (Hz) or s–1 are the units of measurement.

3) Time Period: A wave's period is the amount of time it takes to complete one vibration. time in seconds

4) Velocity: The velocity of a wave is the distance it travels in one second. m/s is the unit of speed.

All types of electromagnetic radiation travel at the same speed in vacuum, which is 3 108 m/s. This is known as the speed of light.

5) Wavelength(: A wavelength is the distance between two consecutive crests or troughs. Angstrom() [1=10–10m] is a unit of measurement.

6) Wave Number: This is the number of wavelengths per centimetre. m-1 is the unit of measurement.

\[\overline \nu   = 1/\lambda \]

6.1 Relationship between Velocity, Frequency & Wavelength

c = $\nu.\lambda$

\[{\text{c}}\]: speed of light i.e. 3 × 108 m/s in vaccum 

\[{{\nu }}\]: frequency;

 λ : wavelength

7. ELECTROMAGNETIC SPECTRUM

The electromagnetic spectrum is the band of radiations created when all electromagnetic radiations are grouped in ascending order of wavelength or decreasing frequency.

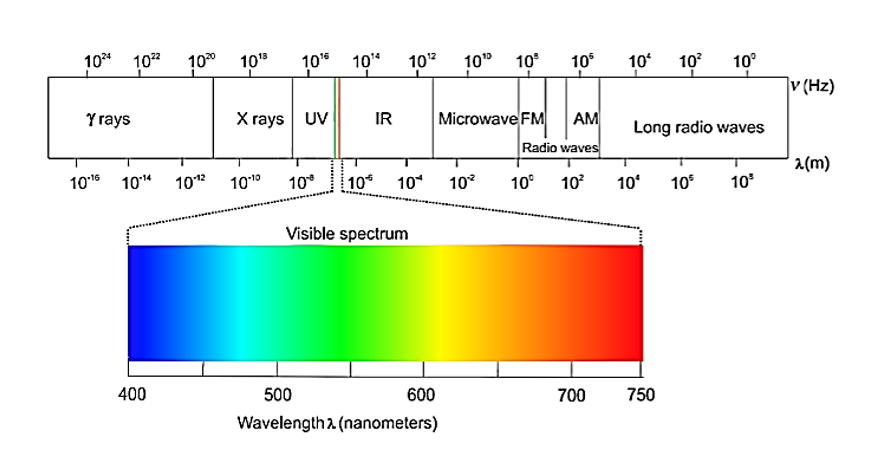
Electromagnetic Spectrum 

The visible spectrum (VIBGYOR) is a subset of this spectrum with a wavelength range of 380-760 nm.

In this order, the wavelengths increase:

Gamma Rays < X-rays < Ultra-violet rays < Visible< Infrared < Micro-waves

7.1 Electromagnetic Wave Theory

(1) A source (such as a heated rod) emits energy continuously in the form of radiations (i.e., there is no change in wavelength or frequency of the emitted radiations as the energy radiated increases).

(2) These are electromagnetically emitted radiations.

7.2 Failure of EM wave theory

Two experiments shattered the theory:

(1) Black Body Radiation: According to Maxwell's theory of body heating, the intensity, or the amount of energy radiated per unit area, should grow without affecting the wavelength or frequency.

However, we notice that when we heat an iron rod, it turns red, then white, and finally blue at extremely high temperatures. The frequency of radiated radiations is shifting because of this.

A black body is an ideal body that produces and absorbs radiation of all frequencies, and the radiation emitted by a black body is known as black body radiation.

The intensity of a black solid varies with wavelength at different temperatures, as seen below:

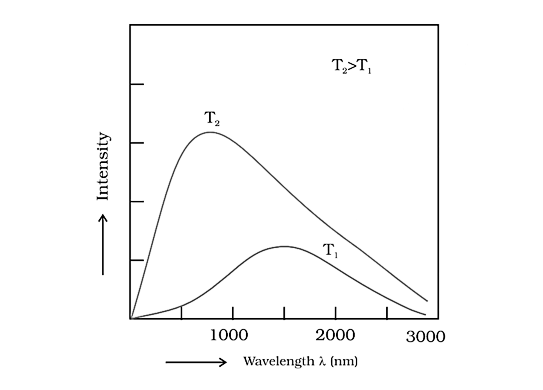
Variation of Intensity of a Black Solid Vs Wavelength at Different Temperatures

As a result, as the temperature rises, the predominate wavelength in the emitted radiations drops while the frequency rises.

At greater temperatures, the intensity increases as predicted by Maxwell's theory, but the wavelength shortens. If \[{{\text{T}}_1} > {{\text{T}}_2} > {{\text{T}}_3}\], the answer is \[{{{\lambda }}_1} < {{{\lambda }}_2} < {{{\lambda }}_3}\].

Photoelectric Effect No. 2

When radiations with a specific minimum frequency (0) strike a metal's surface, electrons are expelled from the metal's surface. The photoelectric effect is the name for this phenomenon. Photoelectrons are the electrons that are released.

According to Maxwell's Theory, electron ejection should be dependent on the intensity of radiation; if electrons are not ejected, raising the intensity will allow them to be ejected.

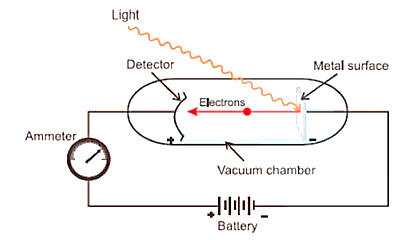
Photoelectric Effect

Following are some observations:

(i) The electrons are ejected from the metal surface as soon as the light beam impacts it, i.e. there is no time lag between the light beam impacting the metal surface and the ejection of electrons.

(ii) The intensity or brightness of light is related to the number of electrons ejected.

(iii) There is a distinctive minimum frequency, 0 (also known as threshold frequency), below which no photoelectric effect is detected for each metal. The expelled electrons have a particular kinetic energy when the frequency is greater than zero. The kinetic energy of these electrons grows as the frequency of light utilised increases.

As a result, these observations ran counter to Maxwell's theory. The number of electrons ejected, and the accompanying kinetic energy should be proportional to the intensity of light. Although the number of electrons emitted is proportional to the brightness of the light, the kinetic energy of the ejected electrons is not.

Max Von Planc's Quantum theory was developed to support these discoveries.

8. PLANCK’S QUANTUM THEORY

The essential points of this theory are:

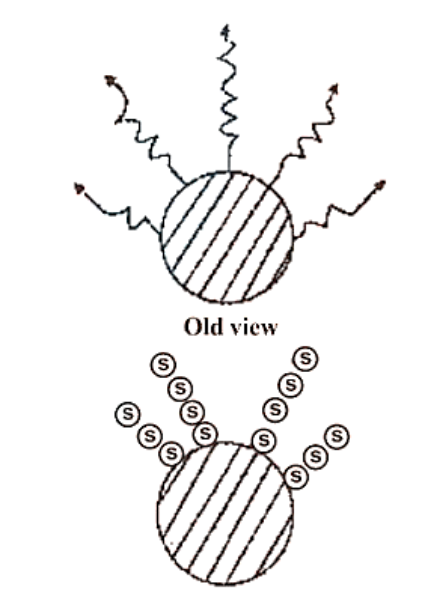
(i) Energy is emitted or absorbed discontinuously in the form of small discrete packets of energy rather than constantly. A 'quantum' is the name given to each such energy packet.

This quantum of energy is known as a photon in the case of light.

Planck’s Quantum Theory: Energy is Emitted or Absorbed Discontinuously in the Form of Small Discrete Packets of Energy Rather than Constantly

(ii) Only one photon can be delivered to one electron or other particle at a time.

(iii) It is impossible to divide or distribute a quantum.

(iv) The frequency of radiation is precisely proportional to the energy of each quantum.

\[{\text{E}}\alpha \nu {\text{ or E = hv = }}\dfrac{{{\text{hc}}}}{\lambda }\]

h = Planck’s constant = \[6.626 \times {10^{ - 34}}{\text{Js}}\]

(v) A body's total energy emitted or absorbed will be quantified in whole numbers.

\[{\text{E = nhv = }}\dfrac{{{\text{nhc}}}}{\lambda }\]

This is also known as "energy quantisation."

8.1 Explanation of Black Body Radiation

The energy emitted increases as the temperature rises, increasing the frequency of the emitted radiations.

The wavelength moves to lower values as the frequency rises.

8.2 Explanation of Photoelectric effect

(i) When a photon of a specific frequency strikes the surface of a metal atom, it imparts all its energy to the metal atom's electron. Only if the photon's energy is high enough to overcome the nucleus's attraction to the electron will the electron be ejected from the metal. As a result, photoelectrons are only expelled when the input light has a minimal frequency (threshold frequency 0). The "Work Function," which is "\[{{\text{h}}_0}\]," is the threshold energy necessary for emission.

(ii) If the incident light's frequency (\[{{\text{v}}_0}\]) exceeds the threshold frequency (\[{{\text{v}}_0}\]), the surplus energy is transferred to the electron as kinetic energy.

Energy of one quantum = Threshold Energy + Kinetic Energy

\[hv = h{v_0}{\text{ + }}\left( {1/{\text{ }}2} \right){m_c}{v^2}{\text{ }}\]

(iii) When, the number of quanta incident increases as the intensity increases, resulting in an increase in the number of photoelectrons expelled.

(iv) When \[{v_0} > v\], the energy of each photon increases, and consequently the kinetic energy of each ejected electron grows as the frequency is increased.

Note:

Energy can also be expressed in Electron Volt(eV).

The energy acquired by an electron when it is accelerated through a potential difference of one volt.

$1{\text{eV}} = 1.602 \times {10^{ - 19}}\;{\text{J}}$

CONCLUSION:

(iii) When, the number of quanta incident increases as the intensity increases, resulting in an increase in the number of photoelectrons expelled.

(iv) When \[{v_0} > v\], the energy of each photon increases, and consequently the kinetic energy of each ejected electron grows as the frequency is increased.

9. WHAT IS SPECTRUM?

A spectrum is a group or band of wavelengths/colors, and spectroscopy is the study of emission or absorption spectra.

9.1 Types of spectrum

Types of spectrums are

1) Emission Spectrum 

2) Absorption Spectrum

9.2 Emission Spectrum

When rays from a source strike a prism and are split into distinct wavelengths before being recorded on a photographic plate.

(a) Continuous Emission Spectra: There are no pauses between wavelengths, and one merges into the next.

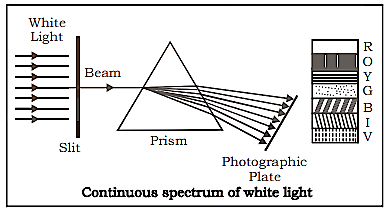
Continuous Emission Spectra of White Light

Discontinuous Emission Spectra, also known as Line Spectra or Atomic Spectra, are a type of continuous emission spectrum.

Certain wavelengths are missing from a group, leaving dark areas in between, causing the spectrum to be discontinuous. It's also known as an element's fingerprint.

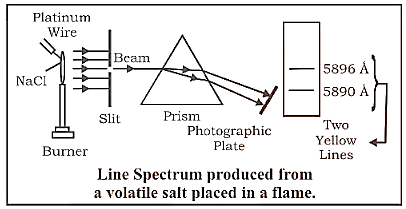
Line Spectrum Produced Form a Volatile Salt Placed in a Flame

9.3 Absorption Spectra

When light from any source is first passed through the solution of a chemical substance and then analysed, it is observed that there are some dark lines in the otherwise continuous spectra.

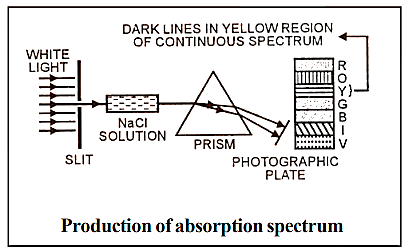
Absorption spectrum

Bohr researched the atomic spectra of hydrogen and offered his hypothesis based on his findings.

10. BOHR’S MODEL

10.1 Postulates

1) An atom is made up of a small, heavy, positively charged nucleus at the centre, which is surrounded by electrons in circular orbits.

2) Electrons can only revolve in orbits with a predetermined energy value. As a result, these orbits are referred to as "energy levels" or "stationary states."

1,2,3,... are the numbers assigned to them. Principal Quantum Numbers are the names given to these numbers.

(a) An electron's energy is given by:

\[{{\text{E}}_{\text{n}}} = {\text{--}}{{\text{R}}_{\text{H}}}\left( {{{\text{Z}}^{\text{2}}}{\text{/}}{{\text{n}}^{\text{2}}}} \right){\text{n  =  1,2,3}}.......\]

where \[{{\text{R}}_{\text{H}}}\] is Rydberg’s constant and its value is 2.18 × 10–18 J.

Z = atomic number

${{\text{E}}_{\text{n}}} =  - 2.18 \times {10^{ - 18}}\dfrac{{{{\text{Z}}^2}}}{{{{\text{n}}^2}}}{\text{J/atom}}$

  ${{\text{E}}_{\text{n}}} =  - 13.6\dfrac{{{{\text{Z}}^2}}}{{{{\text{n}}^2}}}{\text{eV/atom}}$

 $ {{\text{E}}_{\text{n}}} =  - 1312\dfrac{{{{\text{Z}}^2}}}{{{{\text{n}}^2}}}{\text{kJ/mol}}$

As a result, the energies of various levels are arranged in the following order: K L M N...... and so on.

The energy of the lowest state (n=1) is referred to as ground state energy.

(b) Stationary state radiuses:

\[{{\text{r}}_{\text{n}}} =  - \dfrac{{{\text{52}}{\text{.9}}{{\text{n}}^2}}}{{{{\text{Z}}^2}}}{\text{pm}}\]

The radius of the first stationary state for an H-atom (Z = 1) is known as the Bohr orbit (52.9 pm)

(c) Electron velocities in different orbits: 

\[{{\text{v}}_{\text{n}}} = \dfrac{{2.188 \times {{10}^2}}}{{\text{n}}}{\text{m/s}}\]

3) Because electrons can only rotate in orbits with fixed energy values, electrons in an atom can only have certain certain energy values and not any of their own. An electron's energy is so quantified.

4) An electron in an atom's angular momentum, like its energy, can take on specific definite values and not any value at all.

\[{\text{mvr = }}\dfrac{{{\text{nh}}}}{{2\pi }}\]

Where n=1,2,3...... 

5) When an electron is present in the same shell, it does not lose or gain energy.

6) When an electron obtains energy, it is excited to higher energy levels, and when it loses energy in the form of electromagnetic radiations, it is de-excited and returns to lower energy levels.

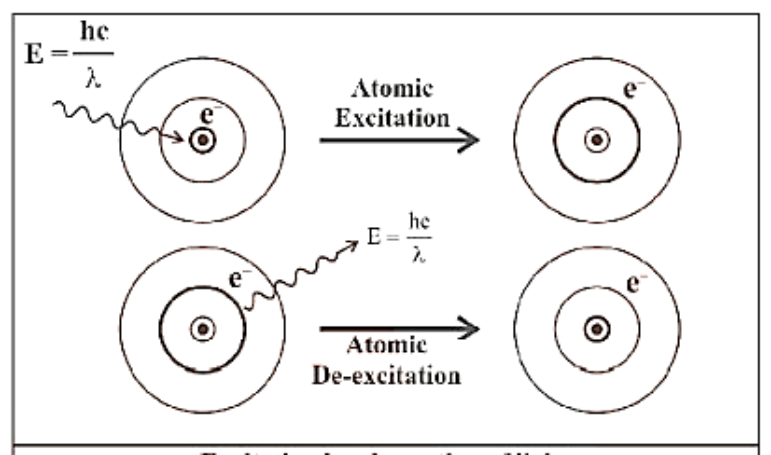
Excitation by Absorption of Light and De-Excitation by Emission of Light

10.2 What does negative energy in the case of the hydrogen atom imply?

The energy of an electron in an atom is lower than the energy of a free electron at rest, as shown by the negative sign. The energy value of a free electron at rest is zero since it is infinitely far away from the nucleus (\[{\text{n = }}\infty \]). En becomes increasingly negative as the electron approaches closer to the nucleus (as n decreases). n=1 corresponds to the most stable orbit and has the largest negative energy value.

Note: Bohr’s model is applicable to H-atom or H-like species like \[{\text{H}}{{\text{e}}^ + }{\text{,L}}{{\text{i}}^{2 + }}{\text{,B}}{{\text{e}}^{3 + }}{\text{ }}\]

10.3 Transition of Electron

${{\Delta  E =  }}{{\text{E}}_{\text{f}}}{\text{ -  }}{{\text{E}}_{\text{i}}}{\text{ }}$

${{\Delta  E =  }}\left[ { - \dfrac{{{{\text{R}}_{\text{H}}}}}{{{\text{n}}_{\text{f}}^2}}} \right] - \left[ { - \dfrac{{{{\text{R}}_{\text{H}}}}}{{{\text{n}}_{\text{i}}^2}}} \right]$

${{\Delta  E =  }}{{\text{R}}_{\text{H}}}\left[ {\dfrac{1}{{{\text{n}}_{\text{i}}^2}} - \dfrac{1}{{{\text{n}}_{\text{f}}^2}}} \right] = 2.18 \times {10^{ - 18}}\left[ {\dfrac{1}{{{\text{n}}_{\text{i}}^2}} - \dfrac{1}{{{\text{n}}_{\text{f}}^2}}} \right]{\text{J/atom}}$

The wavelength associated with the photon's absorption or emission is:

\[\dfrac{{\text{1}}}{{{\lambda }}}{\text{ = }}\dfrac{{{{\Delta E}}}}{{{\text{hc}}}}{\text{ =  }}\dfrac{{{{\text{R}}_{\text{H}}}}}{{{\text{hc}}}}\left[ {\dfrac{1}{{{\text{n}}_{\text{i}}^2}} - \dfrac{1}{{{\text{n}}_{\text{f}}^2}}} \right] = 1.09677 \times {10^7}\left[ {\dfrac{1}{{{\text{n}}_{\text{i}}^2}} - \dfrac{1}{{{\text{n}}_{\text{f}}^2}}} \right]{{\text{m}}^{ - 1}}\]

Rydberg's formula is what it's called.

10.4 Line Spectrum of Hydrogen

The \[{{\text{H}}_2}\] molecules breakdown when an electric discharge is transmitted through gaseous hydrogen, and the energetically excited hydrogen atoms that result generate discrete frequency electromagnetic radiations. Several lines in the hydrogen spectra are named after their discoverer.

Because the energy of an electron cannot change continuously but can only have fixed values, we get discrete lines rather than a continuous spectrum. As a result, the energy of one electron can be quantified.

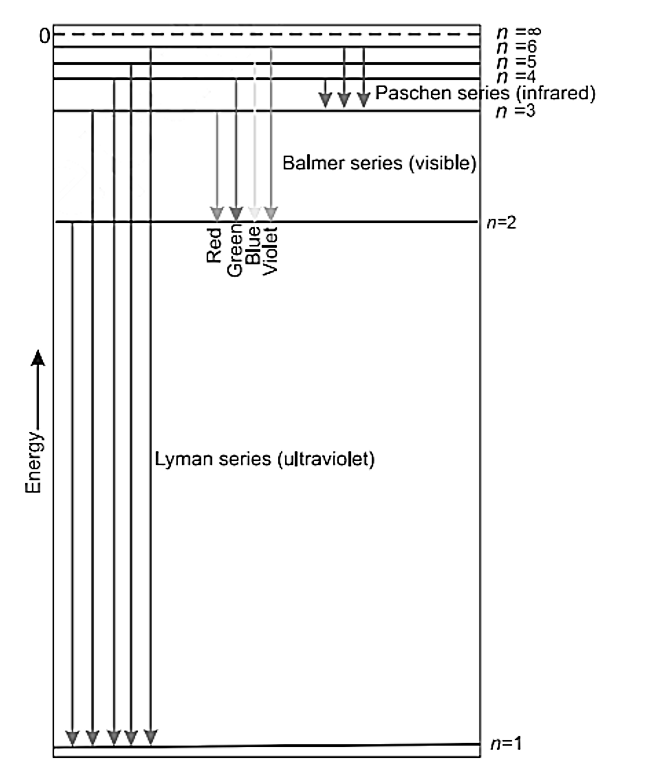
Line spectrum of hydrogen

LYMAN Succession: When an electron jumps from one of the higher states to the ground state or first state (n = 1), a series of ultra violet spectral lines is generated, which is known as the Lyman series.

As a result, according to Rydberg's formula, n1= 1, n2= 2,3,4,5...

BALMER Succession: When an electron goes from a higher state to a state with n=2, a series of spectral lines called the Balmer series is emitted in the visible range.

As a result, according to Rydberg's formula, n1= 2, n2= 3,4,5,6....

PASCHEN Succession: When an electron moves from one of the higher states to the n=3 state, a series of infrared spectral lines is generated, known as the Paschen series.

As a result, n1= 3 and n2= 4,5,6 in Rydberg's formula.

BRACKETT SERIES: When an electron moves from one of the higher states to the state with n = 4, it emits a series of infrared spectral lines known as the Brackett series.

As a result, according to Rydberg's formula, n1= 4, and n2= 5,6,7…

PFUND SERIES: When an electron goes from one of the higher states to the one with n = 4, it emits a series of infrared spectral lines known as the Pfund series. The formula of Rydberg is n1=5,6,7…

Ionization Energy: 10.5

It is the amount of energy necessary to totally remove an electron from an atom and turn it into a positive ion.

$n_1$=1

${{\text{n}}_2} = {\text{ }}\infty$ 

Limiting Line 10.6

It's the shortest wavelength line.i.e., \[{{\text{n}}_2} = {\text{ }}\infty \]

10.7 Limitations of Bohr’s Model

1) Inability to explain multi-electron atom line spectra.

2) It fails to account for the hydrogen spectra's finer characteristics (doublet-two closely spaced lines).

3) Inability to explain line splitting in the magnetic (Zeeman Effect) and electric (Stark Effect) fields- When a source generating radiation is placed in a magnetic or electric field, each spectral line splits up into a number of lines. The Zeeman Effect is the splitting of spectral lines in a magnetic field, while the Stark Effect is the splitting of spectral lines in an electric field.

4) It could not account for atoms' ability to form molecules through covalent connections.

5) He ignores matter's dual behaviour and contradicts the Heisenberg uncertainty principle.

11. QUANTUM MECHANICAL MODELING

This model was built around two ideas:

de Broglie, No. 1

(2) Heisenberg Uncertainty Principle (concept of dual nature of matter)

11.1 Matter's dual behaviour

According to de Broglie, matter should have dual behaviour, i.e. particle and wave-like qualities.

\[\lambda  = \dfrac{{\text{h}}}{{{\text{mv}}}} = \dfrac{{\text{h}}}{{\text{p}}} = \dfrac{{\text{h}}}{{\sqrt {2{\text{m(KE)}}} }} = \dfrac{{\text{h}}}{{\sqrt {2{\text{mq(V)}}} }}\]

Where p denotes a particle's linear momentum.

Every moving item, according to de Broglie, has a wave character. Ordinary objects have wavelengths that are so short (due to their large masses) that their wave characteristics cannot be detected. Electrons and other subatomic particles (with very small masses) have wavelengths that can be measured experimentally.

11.2 Heisenberg's Principle of Uncertainty

It is impossible to measure the position and momentum of a tiny particle with exact precision at the same time. When one of these two parameters is measured with greater precision, the other becomes less precise. The product of positional uncertainty (x) and momentum uncertainty (p) is always a constant and is equal to or larger than \[{\text{h = 4}}\pi \]

$(\Delta {\text{x)}}{\text{.(}}\Delta {\text{p)}} \geqslant {\text{h/4}}\pi$

${\text{or }}(\Delta {\text{x)}}{\text{.(m}}\Delta v{\text{)}} \geqslant {\text{h/4}}\pi$

${\text{or }}(\Delta {\text{x)}}{\text{.(}}\Delta {\text{x)}} \geqslant {\text{h/4}}\pi {\text{m}}$

11.2.1 Explanation

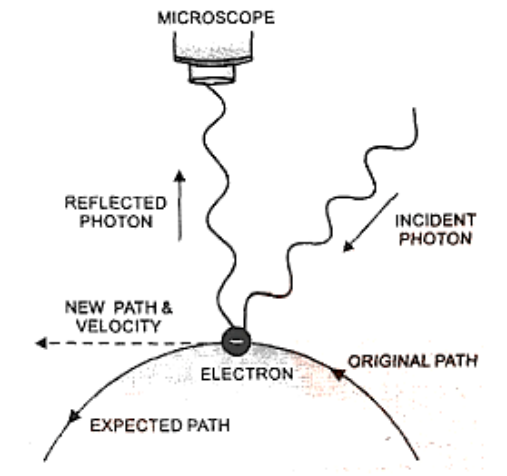
Change of Momentum and Position of Electron on Impact with a Photon

Assume we're attempting to determine an electron's position as well as its momentum. We must utilise light to pin point the position of the electron, so that a photon of light strikes the electron and the reflected photon is seen in the microscope. The electron's location and velocity are both disrupted because of the collision.

11.2.2 The Importance of the Uncertainty Principle:

It eliminates the presence of distinct electron pathways or trajectories, as indicated in Bohr's Model.

12. ATOM QUANTUM MECHANICAL MODEL

Quantum mechanics is a theoretical science that studies the motion of small objects that have both particle and wave features. Schrodinger devised the fundamental equation of quantum mechanics.

The electron wave function $\psi $ is described by this equation. This wave function retains all an electron's information, including its energy, location, and orbital. As a result, it has no physiologic relevance. Quantum Numbers can be used to obtain the information held in about an electron.

Probability: 12.1 The chance of detecting an electron at a given position within an atom is called density $|\psi|^2$.

12.2 Orbital Concept

It's a three-dimensional area around the nucleus where the chances of finding an electron of a certain energy are highest (say upto 90 percent).

Quantum Numbers (12.3)

They can be characterised as a collection of four integers that provide complete information about all the electrons in an atom, such as their location, energy, the type of orbital they occupy, the shape and orientation of that orbital, and so on.

The Schrodinger wave equation yields three quantum numbers: Principal, Azimuthal, and Magnetic quantum numbers. Later, the Spin quantum number, the fourth quantum number, was postulated.

1) Quantum Principal Number (n):

It explains which shell an electron belongs to.

n = 1,2,3,4,5…

Based on electronic leaps between these shells, this number helps to describe the main lines of the spectrum.

(a) It offers the average distance between the nucleus and the electron. The distance from the nucleus increases as n increases.

(b) It determines the energy of a hydrogen atom or a hydrogen-like species fully.

Only the value of n determines the energy of an H-atom or H-like species.

Energy in ascending order: 1, 2, 3, 4, 5, and so on.

The energy of multi-electron species is determined by both the primary and azimuthal quantum numbers.

2n is the maximum number of electrons that can be found in any shell.

2) Azimuthal Quantum Number (l): Orbital Angular Momentum or Subsidiary Quantum Number. Because there are many sub-shells within a single shell, the number of electronic jumps increases, which explains the appearance of tiny lines in the spectrum. This quantum number indicates: 

(a) the number of subshells in a shell; 

(b) An electron's angular momentum in a subshell.

(c) The shapes of different subshells within the same shell.

(d) The relative energies of the different subshells.

Value of l varies from 0 to n – 1 For 1st shell (n = 1): l = 0 

2nd shell (n = 2): l = 0,1 

3rd shell (n = 3): l = 0,1,2 

4th shell (n = 4): l = 0,1,2,3

The initial letters of the words sharp, principal, diffused, and fundamental are represented by the notations s,p,d,f. l = 4 is known as the g subshell, l = 5 is known as the h subshell, and so on.

(3) Magnetic Quantum Number(m):

This quantum number is necessary to explain why, when a line spectrum source is placed in a magnetic field, each spectral line divides into several line segments (Zeeman effect).

Electrons in a subshell can arrange themselves in specific favoured regions of space around the nucleus termed orbitals under the influence of an external magnetic field.

The number of preferred electron orientations in a subshell is determined by the magnetic quantum number.

Because each orientation corresponds to an orbital, the number of orbitals present in any subshell is determined by the magnetic quantum number.

The value of m can be anything between – l and + l, including zero.

Degenerate orbitals are orbitals in the same subshell that have the same energy. Eg In the absence of a magnetic field, the three p-orbitals of a specific main shell have the same energy.

Similarly, the energy of all five d-subshell orbitals of a given shell is the same.

Thus, the sequence of energy for the H-atom is: 1s 2s = 2p 3s = 3p = 3d 4s = 4p = 4d = 4f…

The energy of the orbitals in multi electron atoms falls as the effective nuclear charge increases. Eg

\[{{\text{E}}_{{\text{2s}}}}\left( {\text{H}} \right){\text{  >  }}{{\text{E}}_{{\text{2s}}}}\left( {{\text{Li}}} \right){\text{  >  }}{{\text{E}}_{{\text{2s}}}}\left( {{\text{Na}}} \right){\text{  >  }}{{\text{E}}_{{\text{2s}}}}\left( {\text{K}} \right)\]

Total number of orbitals in each shell = \[{{\text{n}}^2}\] 

Total number of potential m values in each subshell = 2l + 1

4) Spin Quantum Number(s): An atom's electron spins around its own axis in addition to moving around the nucleus. Because an electron in an orbital can spin either clockwise or counterclockwise. As a result, s can only have two values.

\[{\text{ + }}\dfrac{{\text{1}}}{{\text{2}}}{\text{or - }}\dfrac{{\text{1}}}{{\text{2}}}\]

The magnetic characteristics of substances can be explained using this quantum number.

12.4 Shapes of atomic orbitals

(1) S-orbitals have the following shape:

(a) They are non-directional and spherically symmetric, which means that the probability of finding an electron at a given distance is equal in all directions.

(b) The 1s and 2s orbitals have the same shape, but the 2s orbital is larger.

(c) A node is a spherical shell within the 2s orbital where the electron density is zero.

(d) The value of the azimuthal quantum number (l) is zero (l=0), and the magnetic quantum number (m) can only have one value (m = 0).

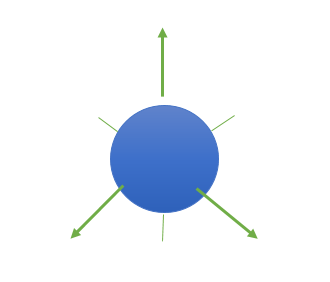
Shape of S-orbital

(2) P-orbital shape: 

(a) It is made up of two lobes on either side of the plane that runs across the nucleus. The p-orbital is formed like a dumbbell.

(b) In p-orbitals, there are three distinct electron cloud orientations. As a result, the lobes of the p-orbital can be thought of as being along the x, y, and z axes. As a result, they are referred to as px, py, and pz. The three p-orbitals are arranged in a right-angle relationship.

(c) There are no p-orbitals in the first main energy level (Principal quantum number n = 1).

(d) Degenerate orbitals are the three p-orbitals of a given energy level that have the same energy in the absence of an external electric and magnetic field.

(e) P-orbitals, like s orbitals, grow as the energy of an atom's primary shell increases. As a result, the value of the azimuthal quantum number is one (l=1), but the magnetic quantum number has three values (m= –1, 0, and +1).

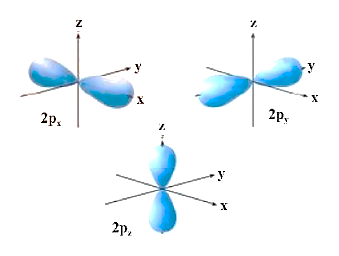
Shape of P-orbitals

(3) D-orbitals' shapes:

(a) They are denoted by the letters \[{{\text{d}}_{{\text{xy}}}}{\text{,}}{{\text{d}}_{{\text{yz}}}}{\text{,}}{{\text{d}}_{{\text{zx}}}}{\text{,and }}{{\text{d}}_{{{\text{x}}^{\text{2}}}{{\text{y}}^{\text{2}}}}}\]. They resemble a four-leaf clover in appearance. The second d orbital, called \[{{\text{d}}_{{z^{\text{2}}}}}\], resembles a doughnut.

(b) In the absence of a magnetic field, all five d orbitals have the same energy.

(c) \[\ell  = 2\] and magnetic quantum number values are –2, –1, 0, + 1,+ 2.

(d) There are no d orbitals in main shells 1 and 2.

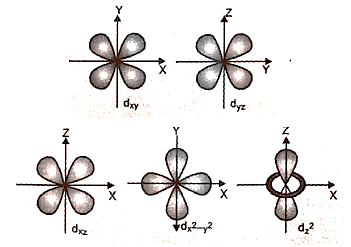
Shape of D-orbitals

We've drawn boundary surface diagrams, in which the surface of an orbital with a constant probability density (\[{\text{\psi }}\])2 is drawn in space. It encloses the area where the chances of detecting the electron are extremely high. We don't construct a boundary surface map that encompasses a 100 percent likelihood of locating the electron since probability density has some value at any finite distance from the nucleus, no matter how small it is. As a result, drawing a boundary surface diagram of a hard size with a 100% likelihood of detecting the electron is impossible.

12.5 Nodes and nodal planes

Node: It's a region where there's no chance of anything happening.

There are two types of nodes: nodes that are connected to each other and nodes that are not connected

(1) Spherical or radial nodes: In an orbital, three-dimensional regions where the probability of locating the electron is zero.

n – \[\ell \] – 1 = number of radial/ spherical nodes

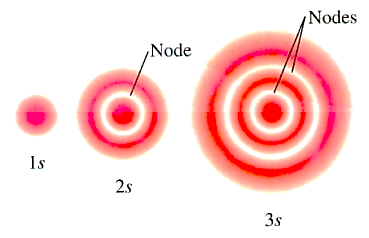
Radial or Spherical Nodes in the Orbitals

(2) Planar or Angular Nodes: These are planes that cut through the nucleus and have no chance of locating an electron.

Nodes with Planar/Angular Shapes: \[\ell \]

n - 1 is the total number of nodes.

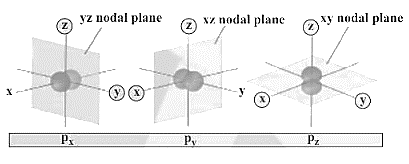
Planar or Angular Nodes

12.6 Filling of orbitals in an atom

(1) The Aufbau Principle 

This principle states that in the ground state of an atom, the orbitals are filled in order of increasing energy. In other words, electrons occupy the lowest energy orbital initially and only enter higher energy orbitals once the lower energy orbitals have been filled.

Unlike the H-atom, where the energy of orbitals is solely determined by n, the energy of multi-electron orbitals is determined by both n and l. The (n+\[\ell \]) rule can be used to calculate their energy ranking. The lower the value of (n+\[\ell \]) for an orbital, the lower its energy, according to this rule. When two different types of orbitals have the same (n+\[\ell \]) value, the orbital with the lower n value has less energy.

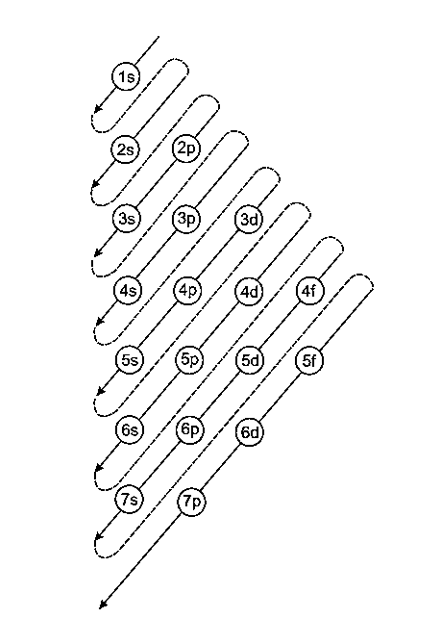
Aufbau Principle for Filling of Electron in the Orbitals

(2) Pauli Exclusion Principle: An orbital can only have two electrons, both of which must have the same spin.

${\text{Correct       }} \uparrow  \downarrow {\text{     or      }} \downarrow  \uparrow$

${\text{                     (i)                (ii)}}$

${\text{Incorrect     }} \uparrow  \uparrow {\text{     or      }} \downarrow  \downarrow {\text{  }}$

$ {\text{                    (iii)               (iv) }} $

(3) Hund's maximum multiplicity rule: Electron pairing in the p, d, and f orbitals can't happen until each subshell's orbital has one electron. All singly occupied orbitals will have parallel spin as well.

12.7 Exceptional Configuration of Cr & Cu

Because of the following reasons, the filled and entirely half-filled subshells are stable:

1. Electron distribution that is symmetrical: It is widely known that symmetry promotes stability. Subshells that are totally filled or half- filled have a symmetrical distribution of electrons and are thus more stable. The energy of electrons in the same subshell (here 3d) is the same, but their spatial distribution is different. As a result, their mutual shielding is minimal, and the electrons are more strongly drawn to the nucleus.

2. Exchange Energy: When two or more electrons with the same spin are present in the degenerate orbitals of a subshell, the stabilising effect occurs. These electrons tend to swap locations, and the energy produced as a result of this swap is known as exchange energy. When the subshell is half-filled or totally filled, the maximum number of exchanges possible is reached. As a result, the exchange energy is at its highest, and the stability is at its best. Eg., \[{\text{Cr}}\] is \[\left[ {{\text{Ar}}} \right]{\text{ 3}}{{\text{d}}^{\text{5}}}{\text{4}}{{\text{s}}^{\text{1}}}\]

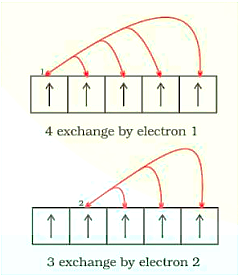
Exchange of Energy by the Electrons in the Orbitals: 4 Exchanges by Elecrron 1; 3 Exchange by Electron 2

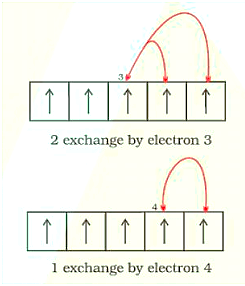
Exchange of Energy by the Electrons in the Orbitals: 2 Exchanges by Electron 3; 1 Exchange by Electron 4

As a result, the total number of exchanges is equal to ten.

12.8 Electronic Configuration of Ions

12.8.1 Cations are generated when an atom's outermost electrons are removed. We must remove the electrons from the highest main quantum number while removing the electrons.

Anions are produced when electrons are introduced to the innermost vacant shell of a molecule.

12.8.3 Magnetic moment: \[\sqrt {{\text{n(n + 2)B}}{\text{.M}}} \]

\[{\text{B}}{\text{.M}}\]is Bohr Magneton

The number of unpaired electrons is given by n.

The term paramagnetic refers to species having unpaired electrons, while diamagnetic refers to species with no unpaired electrons.

Rydberg equation: \[\dfrac{{\text{1}}}{{{\lambda }}}{\text{ =  }}{{\text{R}}_{\text{H}}}\left[ {\dfrac{1}{{{\text{n}}_{\text{1}}^2}} - \dfrac{1}{{{\text{n}}_{\text{2}}^2}}} \right]\]

\[{{\text{R}}_{\text{H}}}{\text{ = 109678c}}{{\text{m}}^{{\text{ - 1}}}}{\text{ and }}{{\text{n}}_{\text{2}}}{\text{ > }}{{\text{n}}_{\text{1}}}\]

$c = \lambda \times \upsilon$  and $\overline {{\nu }} {\text{ = }}\dfrac{{\text{1}}}{{{\lambda }}}$

${\text{E = hv or }}\dfrac{{{\text{hc}}}}{{{\lambda }}}$

Bohr’s Model

${{\text{E}}_{\text{n}}}{\text{ = }}\dfrac{{{\text{ - 1312}}{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^{\text{2}}}}}{\text{kJ mo}}{{\text{l}}^{{\text{ - 1}}}}$

${\text{ = }}\dfrac{{{\text{ - 2}}{\text{.178 \times 1}}{{\text{0}}^{{\text{ - 18}}}}{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^{\text{2}}}}}{\text{J/atom = }}\dfrac{{{\text{ - 13}}{\text{.6}}{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^{\text{2}}}}}{\text{eV/atom}}$

Velocity of electron, \[{{\text{\upsilon }}_{\text{n}}}{\text{ = }}\dfrac{{{\text{2}}{\text{.165 \times 1}}{{\text{0}}^{\text{6}}}{\text{Z}}}}{{\text{n}}}{\text{m/s}}\]

Radius of orbit, \[\dfrac{{0.529{{\text{n}}^2}}}{{\text{Z}}}{\text{{\AA}}}\]

Photoelectric effect \[{\text{h\nu  = h}}{{{\nu }}_{\text{0}}}{\text{ + }}\dfrac{{\text{1}}}{{\text{2}}}{\text{m}}{{{\nu }}^{\text{2}}}\]

\[{{{\nu }}_{\text{0}}}\]= threshold frequency

de-Broglie equation: \[{{\lambda  = }}\dfrac{{\text{h}}}{{{\text{mv}}}}\]

Heisenberg’s uncertainty principle: \[{{\Delta x \times \Delta p}} \geqslant \dfrac{{\text{h}}}{{{\text{4\pi }}}}\]

14. MATHEMATICAL MODELLING OF BOHR’s POSTULATES

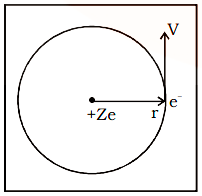
Consider an ion with an atomic number of (Z) and a single electron circling around its nucleus at a distance of 'r', as indicated in the diagram.

Bohr’s Atomic Model

Charge on the nucleus = \[{\text{ + Ze}}\]

The electrostatic attraction (F) between the charge nucleus \[{\text{ + Ze}}\] and the electron (–e) is given by

\[{\text{F = }}\dfrac{{{\text{K}}\left| {{{\text{q}}_{\text{1}}}} \right|\left| {{{\text{q}}_{\text{2}}}} \right|}}{{{{\text{r}}^{\text{2}}}}}\]

Where \[{\text{K = }}\dfrac{{\text{1}}}{{{\text{4\pi }}{{{\varepsilon }}_{\text{0}}}}}\]

${\text{K = }}\dfrac{{\text{1}}}{{{\text{4\pi }}{{{\varepsilon }}_{\text{0}}}}}$

$= 9 \times {10^9}{\text{ N}}{{\text{m}}^2}{{\text{C}}^{ - 2}}$

$ {\text{F = }}\dfrac{{{\text{K}}\left| {{\text{Ze}}} \right|\left| { - {\text{e}}} \right|}}{{{{\text{r}}^2}}} = \dfrac{{{\text{KZ}}{{\text{e}}^2}}}{{{{\text{r}}^2}}}...{\text{(i)}}$

The electron is subjected to centrifugal forces is \[\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{\text{r}}}...{\text{(ii)}}\]

This centrifugal force must be provided by the electrostatic force of attraction (F).

From (i) and (ii), we have :\[\dfrac{{{\text{KZ}}{{\text{e}}^2}}}{{{{\text{r}}^2}}}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{\text{r}}}...{\text{(iii)}}\]

Electron angular momentum around the nucleus

\[{\text{mVr = }}\dfrac{{{\text{nh}}}}{{{\text{2\pi }}}}...{\text{(iv)}}\]

n is a positive integer

\[{\text{n = 1,2,3,}}...\infty \]

solve (iii) and (iv)

\[{\text{V = }}\dfrac{{{\text{2\pi KZ}}{{\text{e}}^{\text{2}}}}}{{{\text{nh}}}}{\text{ r = }}\dfrac{{{{\text{n}}^{\text{2}}}{{\text{h}}^{\text{2}}}}}{{{\text{4}}{{{\pi }}^{\text{2}}}{\text{Km}}{{\text{e}}^{\text{2}}}{\text{Z}}}}\]

Put \[{\text{K = 9 \times 1}}{{\text{0}}^{\text{9}}}{\text{N}}{{\text{m}}^{\text{2}}}{{\text{C}}^{{\text{ - 2}}}}{\text{, e = 1}}{\text{.6 \times 1}}{{\text{0}}^{{\text{ - 19}}}}{\text{C and h = 6}}{\text{.63}} \times {\text{1}}{{\text{0}}^{ - 34}}\]

to get js in the above expressions

Velocity of an electron in \[{{\text{n}}^{{\text{th}}}}\]orbit

\[{{\text{V}}_{\text{n}}}{\text{ = 2}}{\text{.165 \times 1}}{{\text{0}}^{\text{6}}}\dfrac{{\text{Z}}}{{\text{n}}}{\text{m}}{{\text{s}}^{{\text{ - 1}}}}\]

Radius \[{{\text{r}}_{\text{n}}}{\text{ = 0}}{\text{.53}}\dfrac{{{{\text{n}}^2}}}{{\text{Z}}}{\text{{\AA}}}\]

The Total Energy of an electron in the nth orbit is now

${\text{K}}{\text{.E}}{{\text{.}}_{\text{n}}}{\text{ + E}}{\text{.P}}{\text{.E}}{{\text{.}}_{\text{n}}}$

${\text{T}}{\text{.E}}{{\text{.}}_{\text{n}}}{\text{ = }}\dfrac{{\text{1}}}{{\text{2}}}{\text{m}}{{\text{V}}_{\text{n}}}^{\text{2}}{\text{ + }}\dfrac{{{\text{K(Ze)( - e)}}}}{{\text{r}}}\left[ {\because {\text{E}}{\text{.P}}{\text{.E}}{\text{. = }}\dfrac{{{\text{K}}{{\text{q}}_{\text{1}}}{{\text{q}}_{\text{2}}}}}{{\text{r}}}} \right]$

$ {\text{T}}{\text{.E}}{{\text{.}}_{\text{n}}}{\text{ = }}\dfrac{{\text{1}}}{{\text{2}}}\left( {\dfrac{{{\text{KZ}}{{\text{e}}^{\text{2}}}}}{{{{\text{r}}_{\text{n}}}}}} \right){\text{ + }}\dfrac{{{\text{K(Ze)( - e)}}}}{{{{\text{r}}_{\text{n}}}}} $

${{\text{E}}_{\text{n}}} \equiv {\text{T}}{\text{.}}{{\text{E}}_{\text{n}}}{\text{ = }}\dfrac{{{\text{ - KZ}}{{\text{e}}^{\text{2}}}}}{{{\text{2}}{{\text{r}}_{\text{n}}}}}$

The Total Energy of an electron in the nth orbit is now

\[{\text{K}}{\text{.E}}{{\text{.}}_{\text{n}}}{\text{ = }}\dfrac{{\text{1}}}{{\text{2}}}\dfrac{{{\text{KZ}}{{\text{e}}^2}}}{{{{\text{r}}_{\text{n}}}}},{\text{P}}{\text{.E}}{{\text{.}}_{\text{n}}}{\text{ = }}\dfrac{{{\text{ - KZ}}{{\text{e}}^{\text{2}}}}}{{{{\text{r}}_{\text{n}}}}}{\text{ and E}}{{\text{.}}_{\text{n}}} = {\text{ }}\dfrac{{{\text{ - KZ}}{{\text{e}}^{\text{2}}}}}{{{\text{2}}{{\text{r}}_{\text{n}}}}}\]

\[{\text{K}}{\text{.E}}{{\text{.}}_{\text{n}}}{\text{ =  - E}}{{\text{.}}_{\text{n}}}{\text{ and  E}}{\text{.P}}{\text{.E}}{{\text{.}}_{\text{n}}} = {\text{ 2}}{{\text{E}}_{\text{n}}}\]

When we use the value of r n in the \[{{\text{E}}_{\text{n}}}\] expression, we get

\[{{\text{E}}_{\text{n}}} = \dfrac{{{\text{ - 2}}{{{\pi }}^{\text{2}}}{{\text{K}}^2}{\text{m}}{{\text{e}}^4}{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^2}{{\text{h}}^2}}}\]

$ {{\text{E}}_{\text{n}}} = {\text{ - 2}}{\text{.178}} \times {10^{ - 19}}\dfrac{{{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^2}}}{\text{J/atom}}$

${{\text{E}}_{\text{n}}} = {\text{ - 13}}{\text{.6}}\dfrac{{{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^2}}}{\text{eV/atom}}$

${{\text{E}}_{\text{n}}} = {\text{ - 2}}{\text{.178}} \times {10^{ - 19}}\dfrac{{{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^2}}}{\text{J/atom}}$

${{\text{E}}_{\text{n}}} = {\text{ - 13}}{\text{.6}}\dfrac{{{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^2}}}{\text{eV/atom}}$

$\left[ {\because {\text{leV = 1}}{\text{.6}} \times {\text{1}}{{\text{0}}^{ - 19}}{\text{J}}} \right]$

$\equiv  - 2.178 \times {10^{ - 18}}\dfrac{{{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^2}}} \times 6.02 \times {10^{23}}{\text{J/mole}}$

$\equiv {\text{ - 1312}}\dfrac{{{{\text{Z}}^{\text{2}}}}}{{{{\text{n}}^2}}}{\text{kJ/mole}}$

15. PROBABILITY DISTRIBUTION DIAGRAMS FOR 1s AND 2s

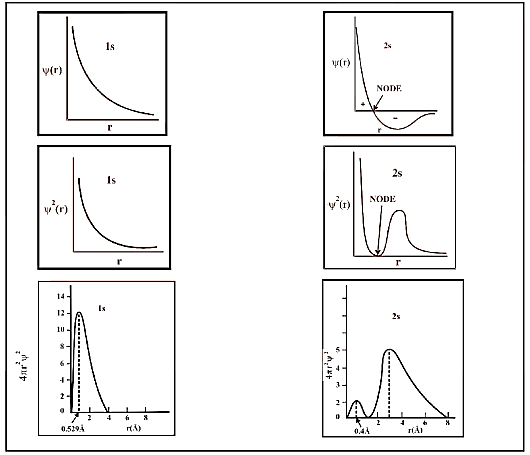
Probability Distribution Diagrams for 1s and 2s

Structure of Atom Class 11 Notes Chemistry - Basic Subjective Questions

Section – A (1 Mark Questions)

1. Which of the following rays/particles will not show deflection from their path on passing through an electric field?

Proton, cathode rays, electron, neutron

Ans. Neutron will not show any deflection from their path on passing through an electric field because neutron is neutral, i.e., chargeless, so no interaction of electric field with neutron occur.

2. An atom having mass number 13 has 7 neutrons. What is the atomic number of the atom?

Ans. Carbon atoms with 7 neutrons have mass number of 13 (6 protons + 7 neutrons = 13). So atomic number of atom will be 6. These atoms are the isotope of carbon called carbon-13.

3. What do you mean by valence electrons?

Ans. The outermost shell of any atom is known as valence shell and the electrons present in this shell are known as valence electrons.

For e.g. Carbon (atomic number Z = 6) ⇒ electronic configuration ⇒ K – 2, L – 4

Thus, L shell is the valence shell and the 4 electrons present in this shell are valence electrons

4. What are the α - particles?

Ans. α-particles are doubly positive charged helium ions (He+2) each having two protons and two neutrons bound together into a particle identical to helium nucleus.

α – Particles ⇒ He+2.

5. Why some atoms shows radioactivity?

Ans. When the number of neutrons exceeds the number of protons in the nucleus of atom, it becomes unstable and shows radioactivity. For e.g., 6C12 has 6 protons and 6 neutrons so it stable while 6C14 has 6 protons and 8 neutrons is unstable and shows radioactivity.

6. What does nucleon contains ?

Ans. Nucleon contains both protons and neutrons

7. Why Bohr’s orbits are called stationary states?

Ans. According to Bohr’s theory, electrons revolve around the nucleus and they have fixed amount of energy. Thus they are called as stationary states.

8. Which of the following orbitals are degenerate $4d_{xy},4d_{yz},4d_{z^2},3d_{xy},3d_{yz},3d_{z^2},$?

Ans. $4d_{xy},4d_{yz},4d_{z^2}$ are degenerate orbitals. $3d_{xy},3d_{yz},3d_{z^2}$ are degenerate orbitals .

9. Nickel atom can lose two electrons to form Ni2+ ion. The atomic number of nickel is 28. From which orbital will nickel lose two electrons?

Ans. The electronic configuration of Ni atom is [Ar]3d84s2. To form Ni2+, it will lose two electrons from 4s orbital to form Ni2+

10. Calculate the total number of angular nodes and radial nodes present in 3p orbital.

Ans. For 3p orbital n=3, l =1.So number of angular nodes = l = 1 and number of radial nodes = n–l–1 = 3–1–1 = 1

Section – B (2 Marks Questions)

11. What is the reason behind fractional atomic mass?

Ans. The reason behind the fractional atomic masses of elements are the different isotopes of an element present in nature. Most of the elements have more than one natural isotope having different masses. Since the atomic mass of an element is the average relative mass of all the natural isotopes of that element.

For e.g., Chlorine in found to exist as two isotopes i.e. Chlorine-35 and Chlorine-37 in ratio of 75% and 25% respectively.

This means that isotope of mass 35 u will contribute 75% whereas isotope of mass 37 u will contribute 25% to average atomic mass of Chlorine.

Average atomic mass of Chlorine = (35 × 75 + 37 × 25)/100

=2625/100 + 925/100

= 26.25 + 9.25

= 35.5u.

Thus, average atomic mass of Chlorine is 35.5 u i.e. in fraction.

12. What is the difference between mass number and atomic mass?

Ans. The difference between mass number and atomic mass is that mass number is always a whole number (because it is number of protons and neutrons) whereas atomic mass is mass of protons and neutrons compared to
C–12 atom. For e.g. mass number of hydrogen is 1 but its atomic mass is 1.008 u.

13. What are the general features of isotope?.

Ans. The general features of isotopes are as follows:

1. The isotopes of an element have same atomic number (i.e. same number of protons in the nucleus and same number of electrons in the extra nuclear part)

2. The isotopes of an element have different mass numbers (i.e. different in the number of neutrons present in the nucleus)

3. Isotopes have same electronic configuration hence share similar chemical properties.

4. Isotopes of an element have different masses, so they have different physical properties like melting point, boiling point, density etc.

5. Due to difference in the nuclear structure (i.e., number of neutrons), they have different nuclear properties, e.g., C–14 isotope is radioactive whereas C–12 isotope is non-radioactive

14. Wavelengths of different radiations are given below :

λ(A) = 300 nm 

λ(B) = 300 μm 

λ (C) = 3 nm 

λ (D) = 30 A°

Arrange these radiations in the increasing order of their energies.

Ans. The energy is inversely proportional to the wavelength 

$E\propto \frac{1}{\lambda}$

λ(B)<λ(A) <λ (C) =λ (D)

15. Calculate the frequency of the radiation emitted when an electron jumps from n = 3 to n = 2 in a hydrogen atom.

Ans. Wavelengths is represented by λ and is given by following expression

$\frac{1}{\lambda}=R \left ( \frac{1}{n^2_1}-\frac{1}{n^2_2} \right )$

$\Rightarrow \frac{1}{\lambda}=\left ( 109677\text{cm}^{-1} \right )\left ( \frac{1}{2^2}-\frac{1}{3^2} \right )$

$\Rightarrow \frac{1}{\lambda}=15232.9167\text{cm}^{-1}$

Frequency v is given by

$\text{v}=\frac{\text{c}}{\lambda}=4.57\times 10^{14}\text{s}^{-1}$

16. Calculate the wavelength and frequency of a light wave whose time period is 2.0 × 10–10 s.

Ans. Given time period = 2.0 x 10-10s we know, 

Frequency (ν) of light $=\frac{1}{\text{Time period}}$, therefore putting the values. We get

$=\frac{1}{2.0\times10^{-10}\text{s} }=5.0\times10^{9}\text{s}^{-1}$

We also know $ \lambda=\frac{\text{c}}{\text{v}}$ 

Where, c = velocity of light in vacuum = $3\times10^{8}\text{m/s}$

Substituting the value in the given expression of $\lambda,$ 

we get $\lambda=\frac{3\times10^8}{5.0\times10^9}=6.0\times10^{-2}\text{m}$

17. Energy of an electron in H atom in ground state is 13.6 eV. What is the value in first excited state?

Ans. Energy of an electron in nth level of H-atom is $\text{E}_{\text{n}}=-\frac{13.6}{\text{n}^2}=\text{eV}$

The energy in first excited state (n = 2), 

$\text{E}_2=-\frac{13.6}{2^2}\text{eV}=-3.4\text{eV}$

18. In the lowest energy level of hydrogen atom, what is the  angular momentum of electron?

Ans. Angular momentum = mvr is an integer multiple of $\frac{\text{h}}{2\pi}$

$\text{mvr}=\frac{\text{nh}}{2\pi}$

For n = 1,\text{mvr}=\frac{\text{h}}{2\pi} 

19. Why was a change in the Bohr Model of atom required? Due to which important development (s), concept of movement of an electron in an orbit was replaced by, the concept of probability of finding electron in an orbital? What is the name given to the changed model of atom?

Ans. Bohr model postulated that electrons move along fixed circular paths which was contradicted by Heisenberg's uncertainty principle and de Broglie concept of dual nature of particle. The concept of movement of electron in an orbit was replaced by concept of probability due to Heisenberg's uncertainty principle. The changed model of atom is called 'wave mechanical model of atom.

20. Show the distribution of electrons in oxygen atom (atomic number 8) using orbital diagram.

Ans. Oxygen is the eight element with a total of 8 electrons. In writing the electron configuration for oxygen the first two electrons will go in the 1s orbital. Since 1s can only hold two electrons the next 2 electrons for O go in the 2s orbital. The remaining four electrons will go in the 2p orbital. Therefore, the O electron configuration will be 1s22s22p4.

PDF Summary - Class 11 Chemistry Structure of Atom Notes (Chapter 2)

Class 11 Chemistry Chapter 2 Structure of Atom is an important chapter, and it is likely to prepare you for advanced concepts based on the atomic model. For instance, the bonding of elements by sharing electrons is included in organic chemistry, which is yet again an essential part of Chemistry as a whole.

It is the central chapter in Physical Chemistry and understanding its basic concepts will help you in sailing through other sections which are included in the syllabus. There are several models of atomic structure proposed by various scientists to suit their theories. Students can refer to our Atomic Structure Class 11 Notes PDF and have a clear understanding of all such models and draw conclusions accordingly while answering questions relating to these topics.

Important Topics Covered Under Chemistry Class 11 Chapter 2 Notes

Notes of Chemistry Class 11 Chapter 2 cover all the important topics that students need to prepare well. Thus once undergoing revision, they can refer to these notes to give precise answers to the questions. Below are the important topics that are covered under Chemistry Class 11 Chapter 2 notes.

• A Basic Introduction About Atoms

• What are atoms?

• What are the subatomic particles of an atom?

• Other basic definitions of subatomic particles

• Thompson Model

• Rutherford’s Model

• Atomic Mass And Atomic Number

• What are electromagnetic radiations?

• Electromagnetic Spectrum

• Planck's Quantum Theory

• Spectrum

• Bohr’s Model

• Quantum Mechanical Model

• Probability Distribution of 1s and 2s

Important Questions from Structure of Atom (Short, Long & Practice)

Short Answer Type Questions

1. How many total electrons are present in nitrate ions?

2. What are nucleons?

3. Write electronic configurations of Chromium.

Long Answer Type Questions

1. How many nucleons are present in an atom Nobelium, No? How many electrons are present in the atom? How many nucleons may be considered neutrons?

2. A particular radio station broadcasts at a frequency of 1120 kHz (kilohertz). Another radio station broadcasts at a frequency of 98.7 MHz (megahertz). What are the wavelengths of the radiations from each station?

3. The wavelength of the first line in the Balmer Series is 656 nm. Calculate the wavelength of the second line and limiting line in the Balmer series.

Practice Questions

1. Write down the electronic configuration of Cu (= 29) in the ground state.

2. How many quantum numbers are required to specify an orbital? Name them.

3. Arrange the following orbitals in the order in which electrons may be normally expected to fill them.

3s, 2p, 3p, 2s, 3d, 4s.

4. Which fundamental property of an atom is not understood if we assume that an atom consists of a nucleus containing protons only and an extranuclear part containing an equal number of electrons?

5. Calculate the wavelength of the spherical line in the Lyman series corresponding to n2 = 3.

Key Features of Revision Notes for Class 11 Chemistry Chapter 2 - Structure of Atom

• TheRevision Notes for Class 11 Chemistry Chapter 2 Structure of Atom are written by experts at Vedantu and all the points are accurate.

• Every point is clear as it is written in easy to understand language.

• These notes are useful for students from both board and competitive exam point of view.

• Reactions are explained to make students understand concepts in a better way.

• Revision Notes for Class 11 Chemistry Chapter 2 - Structure of Atom are absolutely free and available in PDF format for download.

Class 11 Chemistry Revision Notes

Conclusion

Vedantu now has the Structure of Atom revision notes in PDF format. These Revision Notes were created by master teachers, so students can trust them. From an exam perspective, we have also provided additional questions on this page. These notes and key questions can be used by students to prepare for exams and review certain subjects.