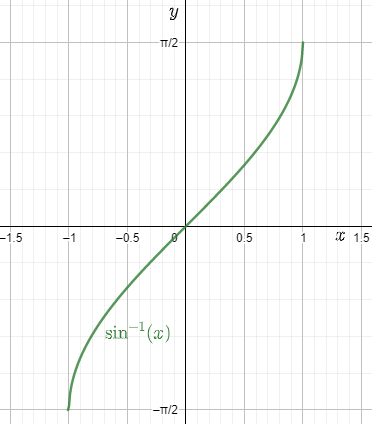
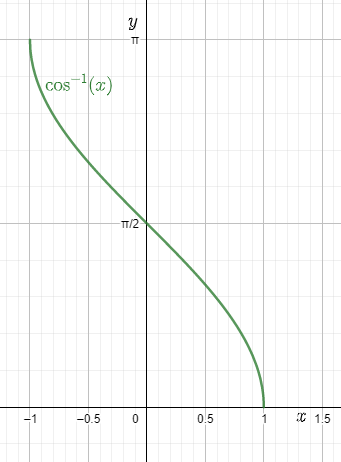
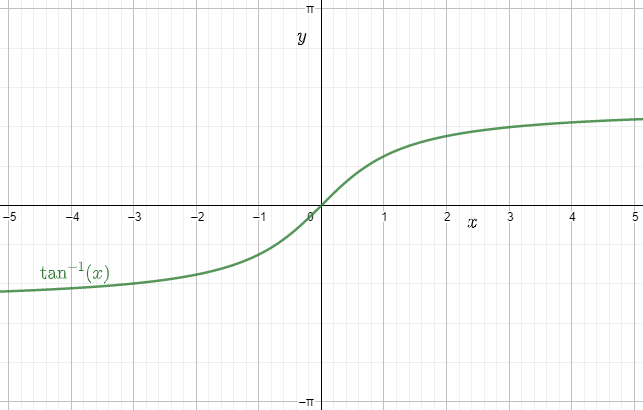
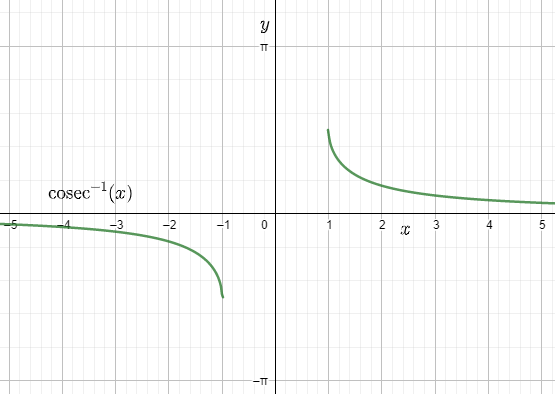
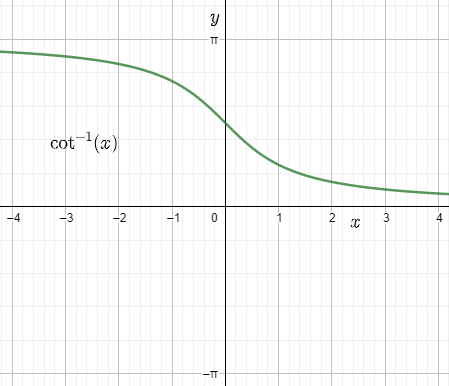
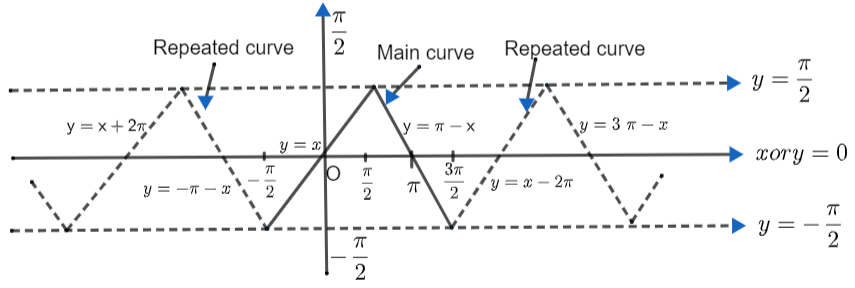
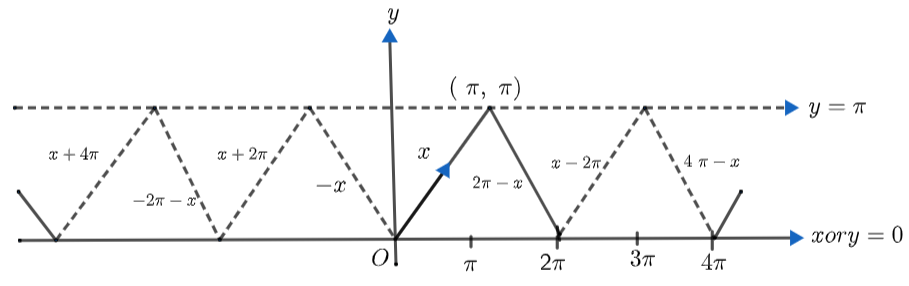
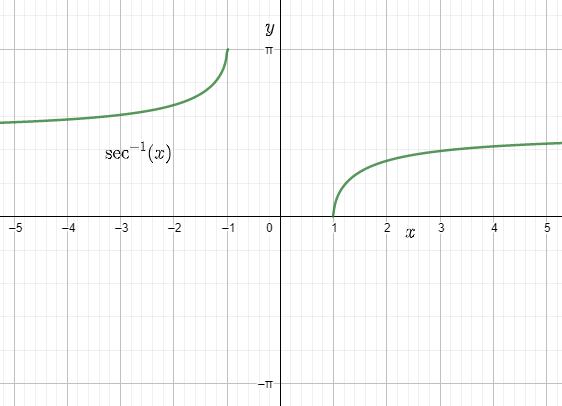Maths Chapter 2 Inverse Trigonometric Functions Class 12 Notes Download FREE PDF



FAQs on Inverse Trigonometric Functions Class 12 Notes: CBSE Maths Chapter 2
1. Find the value of x, if sin (x) = 2 in Inverse Trigonometric Functions Notes.
We know that sin x = 2,
X = sin-1 (2), this is not possible
This means that there is no value of x for which sin x = 2. This is true since the domain of sin-1x is -1 to 1 for the value of x.
2. What is the value of sin-1 (sin (π / 6)) form Inverse Trigonometric Functions Notes?
sin-1 (sin (π / 6)) = π / 6
We have arrived at the above answer by using the sin-1 (sin (x) ) = x identity.
3. What is the value of sin (cos-1 3 / 5) in Inverse Trigonometric Functions Class 12 Notes PDF?
Let’s suppose that cos-1 3 /5 = x
This means that cos x = 3 / 5
We also know that sin x = √1 - cos2 x
So, sin x = √1 - 9 / 25 = 4 / 5
This means that sin x = sin (cos-1 3 / 5) = 4 / 5.
4. Find the value of sin (cot - 1x) from Inverse Trigonometric Functions Notes.
Let’s assume that cot-1 x = θ
X = cotθ
Now, cosec θ = √1 + cot2θ = √1 + x2
Hence, sinθ = 1 / cos ec θ = 1 / √1 + x2
Θ = sin-1 1 / √1 + x2
Hence, sin (cot - 1x) = sin (sin-1 x 1 / √1 + x2 = 1 /√ 1 + x2 = (1 + x2)-1 / 2.
5. What is the value of sec-1
sec(−30degrees)
sec(−30degrees) in Inverse Trigonometric Functions Notes.
sec-1 [sec (-30 degrees)] = sec-1 (sec 30 degrees) = 30 degrees.
6. Where can I download the latest Chapter 2 Inverse Trigonometric functions of Class 12 Maths notes?
You can download the Inverse Trigonometric Functions Class 12 Notes PDF from the Vedantu website. Here at Vedantu, you will find all revision notes from which you can study.
Click on the download pdf option.
Once the revision notes pdf is saved on your device, you can use it to study later offline.
7. What are the various functions discussed in Chapter 2 Inverse Trigonometry Class 12 Notes?
As per the syllabus of Class 12 Maths CBSE, the second chapter in the Maths textbook of Class 12 is inverse trigonometric functions. Previously, you have learnt about trigonometric functions and keeping that knowledge and concepts in mind, you will easily be able to understand this particular chapter. You will learn about the inverse functions of trigonometry like arcsine, arctangent, arccosine, arccotangent, arcsecant, arccosecant functions. You will need to understand these topics to solve the sums from the chapter.
These solutions are available on Vedantu's official website(vedantu.com) and mobile app free of cost.
8. What are the topics in Chapter 2 Inverse Trigonometry Class 12 Notes?
Chapter 2 Inverse Trigonometric functions of Class 12 Maths deals with the Inverse Trigonometric Functions. You will have to study various subtopics like inverse functions, equations using these inverse functions, and the graphs pertaining to these. You will also have to memorize the important formulas given in the chapter to be able to solve the questions. You must be acquainted with the notations and symbols for the various functions so that it becomes easier to move forward.
9. How can I get all trigonometry questions right in the Class 12 Maths exam?
It is not a very big deal to be able to get all the sums correct from the trigonometry section in your board exam. The key to getting full marks is practice. You must be consistent with your practice and solve as many sums as possible from the trigonometry chapter in order to be confident and accurate. This will enhance your concepts and problem solving skills as well. Apart from this, you must not forget to refer to mock papers and previous year papers to understand the pattern and prepare accordingly.
10. What is meant by inverse trigonometric functions according to Chapter 2 Inverse Trigonometry Class 12 Notes?
In your previous chapter, you gathered ideas about the normal trigonometry, its functions, derivatives etc. Now when you study inverse trigonometry, it is nothing but the inverse or the reciprocal of the actual one. That is, all the functions, angles, derivatives, formulas etc. everything will be written as the reciprocal or opposite of the corresponding trigonometric functions, angles, derivatives , formulas etc. You must refer to the Vedantu explanation of this chapter in order to understand clearly.