Maths Notes for Chapter 6 Application of Derivatives Class 12 - FREE PDF Download



FAQs on Application of Derivatives Class 12 Maths Chapter 6 CBSE Notes - 2025-26
1. What is the core concept of Application of Derivatives for Class 12?
The core concept is using derivatives to analyse the behaviour of functions and solve real-world problems. This chapter explores how the derivative of a function, which represents its rate of change, can be used to determine key properties like the slope of tangents, intervals where a function is increasing or decreasing, and points of local maxima and minima.
2. How can I quickly revise the topic of tangents and normals using these notes?
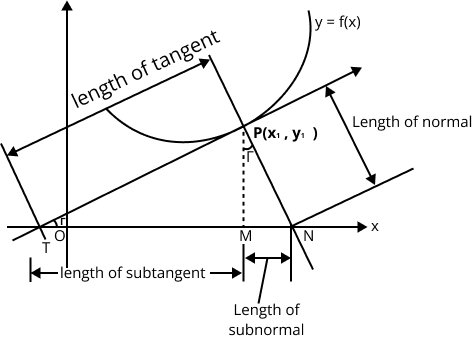
For a quick revision, remember that the derivative, dy/dx, at a point (x₁, y₁) gives the slope of the tangent to the curve at that point. The slope of the normal is the negative reciprocal, -1/(dy/dx). With these slopes, you can use the point-slope form to write the equations for both the tangent and the normal, a key summary point in these notes.
3. What is the main idea behind using derivatives to find the rate of change?
The derivative dy/dx represents the instantaneous rate of change of a quantity 'y' with respect to another quantity 'x'. For revision, focus on how this is applied in problems involving, for example, the rate of change of a circle's area with respect to its radius or the rate of change of a sphere's volume with respect to time.
4. What are the key conditions for determining if a function is increasing or decreasing?
To quickly summarise the concept for revision:
- A function f(x) is strictly increasing on an interval if its derivative, f'(x) > 0 for all x in that interval.
- A function f(x) is strictly decreasing on an interval if its derivative, f'(x) < 0 for all x in that interval.
- If f'(x) = 0, these are critical points where the function's behaviour might change.
5. What is the practical difference between Rolle's Theorem and the Lagrange's Mean Value Theorem (LMVT)?
The main difference lies in their conditions and conclusions. Rolle's Theorem is a special case of LMVT which requires an additional condition: f(a) = f(b). This leads to the conclusion that there is at least one point 'c' where the tangent is horizontal (f'(c) = 0). LMVT does not require f(a) = f(b) and concludes that there's a point 'c' where the tangent's slope is equal to the average slope of the secant line connecting the endpoints.
6. How are the concepts of tangents, increasing/decreasing functions, and maxima/minima connected?
These concepts are all connected through the sign of the first derivative, f'(x). The derivative gives the slope of the tangent. When the slope is positive (f'(x) > 0), the function is increasing. When the slope is negative (f'(x) < 0), the function is decreasing. A point of maxima or minima occurs where the slope changes sign, which happens at a critical point where the tangent is often horizontal (f'(x) = 0).
7. In what situations might the second derivative test for maxima and minima fail, and what is the next step for revision?
The second derivative test fails if, at a critical point 'c' (where f'(c) = 0), the second derivative is also zero, i.e., f''(c) = 0. In this situation, the test is inconclusive. For revision, you must then revert to the first derivative test. Check the sign of f'(x) to the left and right of the critical point 'c' to determine if it is a local maximum, minimum, or a point of inflection.
8. What are the key formulas from this chapter that should be part of a quick revision summary?
For a quick revision of Application of Derivatives, focus on these essential formulas:
- Equation of Tangent: (y - y₁) = m(x - x₁), where m = (dy/dx) at (x₁, y₁).
- Equation of Normal: (y - y₁) = (-1/m)(x - x₁).
- Second Derivative Test: At a critical point c, if f''(c) > 0, it's a local minimum. If f''(c) < 0, it's a local maximum.
- LMVT Condition: f'(c) = (f(b) - f(a)) / (b - a).
9. How do you find the absolute maximum and minimum values of a function on a closed interval [a, b] for a quick concept recap?
To find the absolute extrema, follow this summary:
- Find all critical points of the function within the interval (a, b) by solving f'(x) = 0.
- Evaluate the function's value at these critical points.
- Evaluate the function's value at the endpoints of the interval, f(a) and f(b).
- The largest value from steps 2 and 3 is the absolute maximum, and the smallest value is the absolute minimum.