Maths Notes for Chapter 8 Application of Integrals Class 12 - FREE PDF Download
FAQs on Application of Integrals Class 12 Maths Chapter 8 CBSE Notes - 2025-26
1. What are the main concepts covered in the Application of Integrals Class 12 Revision Notes?
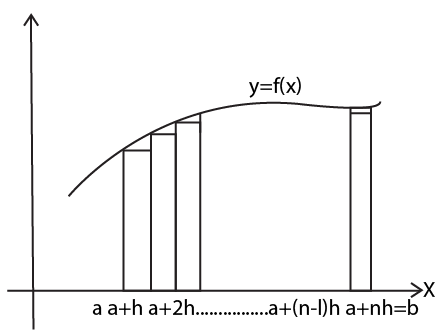
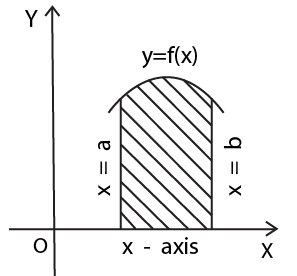
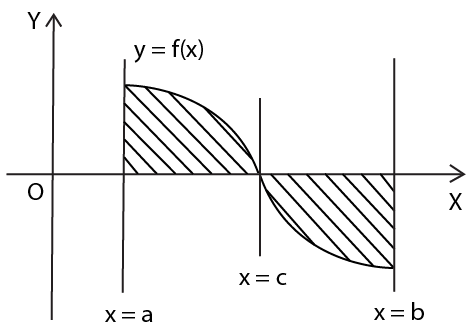
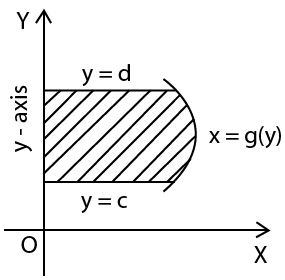
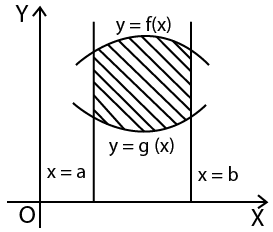
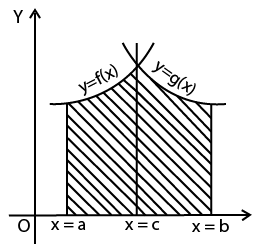
Application of Integrals Class 12 Revision Notes summarize essential concepts such as calculating the area under curves, areas between curves, volume of solids of revolution, and length of curves. The notes also outline theorems and formulas needed to apply integrals in different problem scenarios as per the CBSE 2025–26 syllabus.
2. How can I use the revision notes to quickly revise Class 12 Maths Chapter 8 before exams?
To revise efficiently, start by reviewing the key formulas and concepts highlighted in the notes. Focus on summary sections and solved examples to reinforce understanding of crucial steps. Practise concept maps or flowcharts if provided, as these help visualize relationships between ideas for rapid last-minute revision.
3. What is the quickest way to recall the most important formulas from Application of Integrals for Class 12 exams?
Use these strategies for quick recall:
- Write a formula sheet using your revision notes.
- Group formulas by application: area under curves, area between curves, volumes, and curve lengths.
- Practise one or two representative problems for each formula type from your notes.
- Recite formulas and their use-cases aloud or create mnemonic devices for complex ones.
4. How do the revision notes help connect Application of Integrals to other topics in Class 12 Maths?
Revision notes often show how the application of integrals builds upon earlier topics like functions, differentiation, and basic integration. They may also link to related chapters such as differential equations and area/volume problems in coordinate geometry, providing a holistic understanding and aiding integrated revision.
5. What is a concept map, and how can it help in revising the Application of Integrals chapter?
A concept map is a visual summary that organizes key ideas, formulas, and their interconnections. In Application of Integrals, a concept map can outline when to use area under a curve versus area between curves or indicate conditions for applying each formula. Using such maps from revision notes helps in structuring your study and quickly revising relationships between topics.
6. Why is it important to focus on properties and theorems in Application of Integrals during revision?
Theorems and properties provide shortcuts and logical rules that simplify complex problems, such as symmetry, periodicity, and definite integral properties. Understanding these not only reduces calculation errors but also enables you to tackle unfamiliar questions in exams confidently, as required by the CBSE Class 12 syllabus.
7. How should key terms and definitions be revised for Application of Integrals in Class 12?
Highlight key terms like definite integral, curve tracing, area between curves, limits of integration, and their definitions in your revision notes. Make short notes or flashcards for these terms and quiz yourself to ensure clarity, focusing on their mathematical meaning and how they appear in exam questions.
8. What are effective revision tips for mastering Application of Integrals, according to the notes?
- Start with basic definitions and properties before moving to solved examples.
- Attempt different types of questions, including HOTS and past exam problems, using only the formulas and steps provided in your revision notes.
- Regularly summarize what you have revised in your own words to test understanding.
- Use graphs and diagrams alongside algebraic solutions for better concept retention.
9. How do the Revision Notes help clarify common misconceptions in Application of Integrals?
Revision Notes for Application of Integrals often highlight common errors, such as mixing up the order of upper and lower limits, applying the wrong area formula, or misusing properties for even and odd functions. By emphasizing these areas, the notes guide you to focus on crucial differentiators that prevent mistakes and strengthen conceptual understanding.
10. What type of questions should students expect in the exam after revising from Application of Integrals revision notes?
After revising with the Class 12 Application of Integrals notes, students can expect questions involving:
- Calculation of area under standard curves
- Finding area between two intersecting curves
- Application of properties of definite integrals
- Problem-solving using key theorems from the notes
- Short conceptual and HOTS questions based on symmetry, periodicity, and error identification as outlined for the CBSE 2025–26 board exam