Physics Chapter 12 Atoms Class 12 PDF Download for FREE



FAQs on Atoms Class 12 Notes: CBSE Physics Chapter 12
1. How Can I Download the Revision Notes for Atoms Physics Class 12 Notes PDF from Vedantu?
The following are the steps to download the study materials from Vedantu.
Go to our website Vedantu.com and search for the desired study materials.
You will get a particular link for downloading those study materials.
After clicking on the ‘DOWNLOAD MY PDF’ option, you will get a download link of revision notes as a mail and as a text message on your registered mobile number.
You can click on that link to download notes at your convenience.
2. Write the Bohr’s Quantization condition for the angular momentum of an e- in the 2nd orbit in Chapter 12 Atoms Physics Class 12 Notes PDF.
The formula for angular momentum is:
Here,
So,
3. According to Atoms Notes Class 12 PDF what Do You Mean by Bohr’s Radius?
We define Bohr’s radius as the radius of the first orbit of the hydrogen atom. It is equal to 5.29 x 10-11m ~ 0.53 Å.
4. Can I get answers to Class 12 Physics Board Paper 2024 in Vedantu?
Yes, You can get the answers to the Class 12 Physics Board Paper 2024.
All you have to do is, search for an option of ‘CBSE Class 12 Physics PYQP 2024’ on our website, and you will get the links of PDF files of all the sets of solved class 12 physics board paper 2024.
5. What is the Plum Pudding model according to Chapter 12 Atoms of Class 12 Physics?
Plum Pudding Model is another name given for Thomson’s Model. In Chapter 12 of Class 12 Physics, you will learn about the various atomic model theories right from the very beginning. One of them is the Thompson Model. In this model, it is considered that the atom is like a plum or a watermelon. Like in watermelon or plum, there is a reddish orangish fleshy area and seeds are embedded in it. Thompson considered that the fleshy part is the positive charge of the atom and the seeds resembled the negatively charged electrons.
These solutions are available on Vedantu's official website (vedantu.com).
6. Can I score full marks in Chapter 12 Atoms of Class 12 Physics?
Scoring full marks in your board exams is possible as long as you study and understand the concepts well. If you put in hard work then scoring full marks in any chapter is not a big deal. And the matter with Physics chapter 12 is no different in this case of scoring marks. Physics being a science subject is all about facts and figures and to get this information right in your exam paper, you will need to have all your concepts crystal clear and also a strong base that will give you confidence in attempting all the questions and solving them correctly.
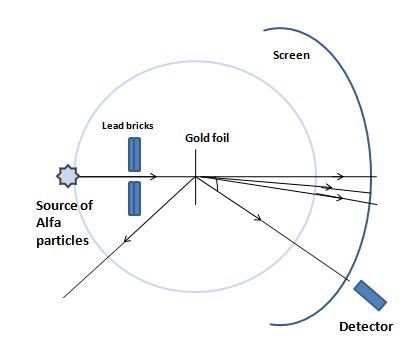
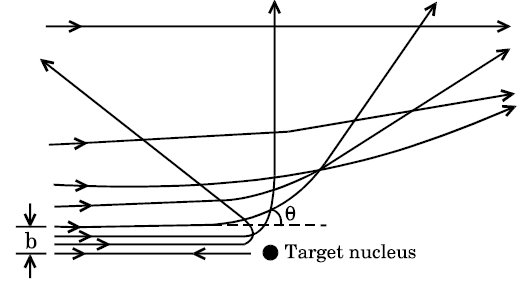
7. What is the Rutherford model according to Chapter 12 Atoms of Class 12 Physics?
Among the many atomic models, one of the distinctive model theories is the one given by Rutherford. Here, in this theory, the atom was understood to be a small spherical region that had its core dense and positively charged, also known as the nucleus. This is compared to the sun and just like the planets revolve around the sun in particular orbits, similarly, the electrons are assumed to revolve around the nucleus in fixed orbits. This is what the Rutherford model is about.
8. Where can I download the latest Chapter 12 Atoms of Class 12 Physics revision Notes?
The Class 12 Physics Chapter 12 Revision Notes are available for download on the Vedantu website. These notes are beneficial as they will clear your concepts and help you form a strong base in Physics to score good grades in your exam.
First, you can click here.
A page from the website will open.
Here you will find the revision notes and the download option.
You can then download and study.
9. What are the various atomic models according to Chapter 12 Atoms of Class 12 Physics?
Chapter 12 of Physics in Class 12 CBSE is called “Atoms”. In this chapter, the various atomic model theories proposed by various physicists are discussed. You can find the topic wise explanation on Vedantu as well, in case you need to brush up on the topics quickly. Some of the model theories discussed are the Thomson’s Model of Atom, Rutherford Atomic Model and Bohr’s Model of Atom also known as Bohr’s theory, proposed by Neil Bohr.
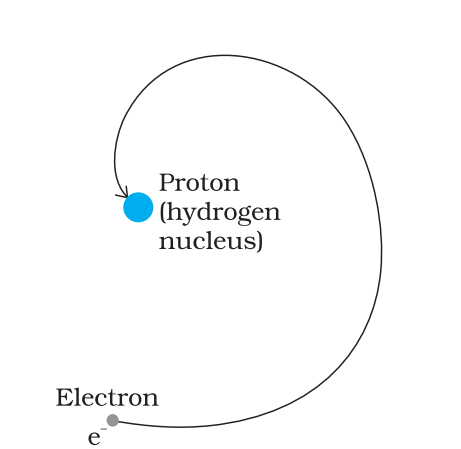
10. Class 12 Physics Chapter 12: What is the Bohr Model of the Atom?
The Bohr Model describes the atom as having a central nucleus surrounded by electrons in fixed orbits. It explains how electrons can only occupy specific energy levels.
11. Class 12 Physics Chapter 12: How do you calculate the radius of an electron’s orbit in the Bohr Model?
You can calculate the radius using the formula
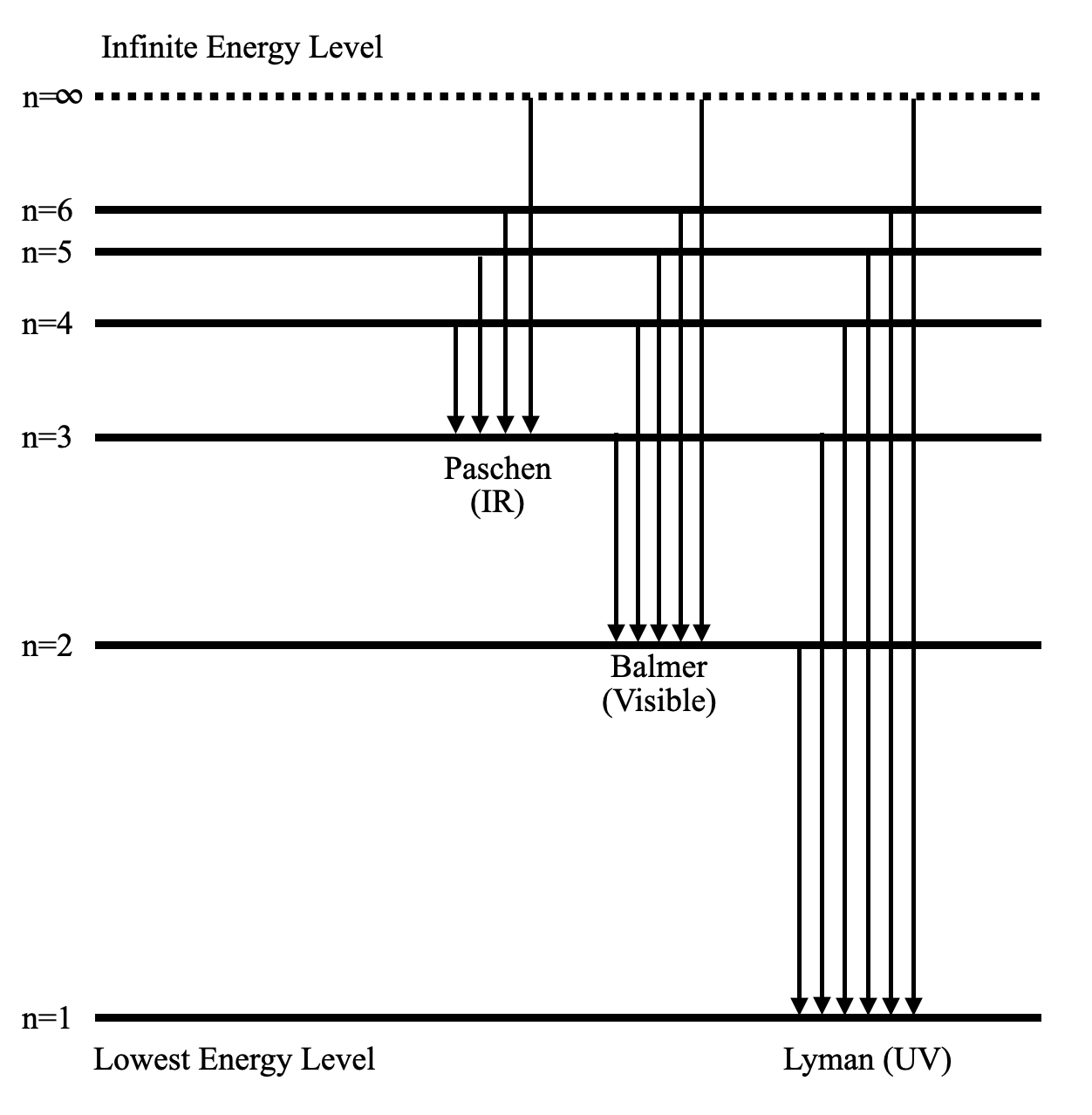
12. Class 12 Physics Chapter 12: What is the significance of spectral lines in atomic theory?
Spectral lines are produced when electrons transition between different energy levels. They help identify elements and understand atomic structure.
13. Class 12 Physics Chapter 12: How do you use the Rydberg formula to find the wavelength of spectral lines?
The Rydberg formula is used to find the wavelength of spectral lines by plugging in the principal quantum numbers of the energy levels into the formula
14. Class 12 Physics Chapter 12: What does de Broglie’s hypothesis tell us about electrons?
De Broglie’s hypothesis suggests that electrons have wave-like properties. It relates their wavelength to their momentum using the formula