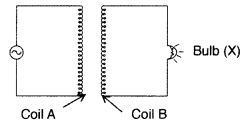
Physics Chapter 7 Notes of Alternating Current Class 12 PDF Download for FREE



FAQs on Alternating Current Class 12 Notes: CBSE Physics Chapter 7
1. What is the difference between alternating current and direct current in Class 12 Physics Chapter 7?
If you study Class 12 Physics Alternating Current notes, you will find out that alternating current changes its polarity whereas direct current maintains the same polarity throughout the time of flow.
2. Are the Class 12 Physics Chapter 7 notes helpful for the exam preparation?
Yes, the Class 12 Physics Chapter 7 notes are helpful for the exam preparation. By referring to the Physics Chapter 7 Class 12 notes, you can solve all the questions in the exercise, and revise the chapter. This is how you can easily complete the chapter and build a strong base on this topic.
3. What are the most important definitions that come in Chapter 7 of Class 12 Physics?
‘Alternating Current’ is a chapter with many and completely new concepts that are unfamiliar to Class 12 students. So, for easy understanding the chapter notes are condensed in the revision notes, but the following list contributes to certain key definitions in the chapter:
Alternating current
Transient current
Inductive and Capacitive reactance
Impedance
RC Circuit
LC Circuit
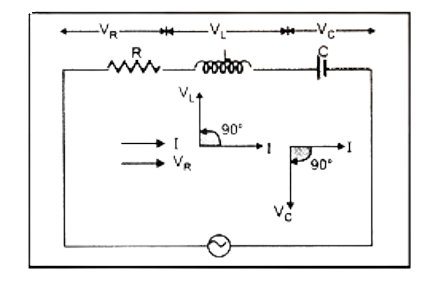
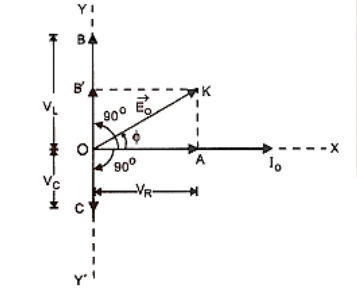
LCR Circuit
Resonance
DC Motor
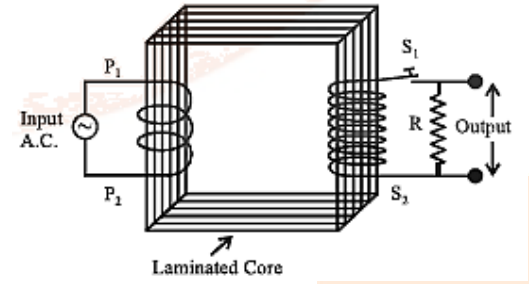
Types of Transformers
Vedantu’s revision notes do a good job of conveying all these concepts in a student-friendly manner.
4. What are the advantages in using the revision notes for studying Chapter 7 of Class 12 Physics?
For the chapter ‘Alternating Current’, revision notes for Class 12 Physics is a material that can be used as a study guide for tests. Vedantu's Notes are among the best because they are developed by in-house professionals who are knowledgeable about the topics related to and prepare the content in an easy and understandable manner. These notes include simple modifications and notes for students to easily understand the concepts such that they can use this right before their tests.
5. What are some important topics in Chapter 7 of Physics for Class 12?
An electric current with continuously changing magnitude and direction periodically in time is called an alternating current. The chapter highlights how AC voltages are preferred over DC because of ease in voltage conversion. The best material that students can get their hands on for reference is revision notes. Below list is a compilation of important topics in Alternating Current:
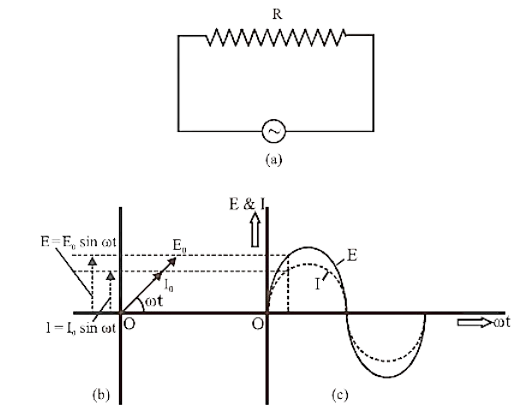
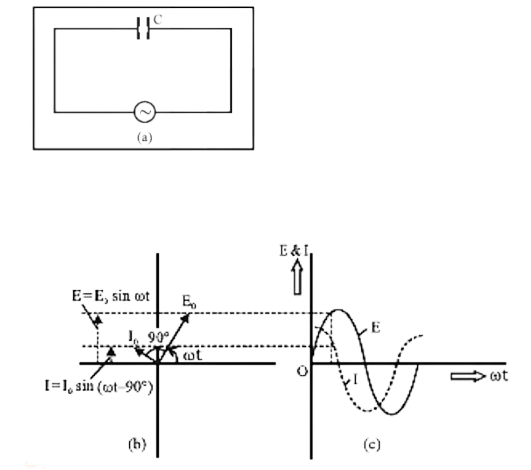
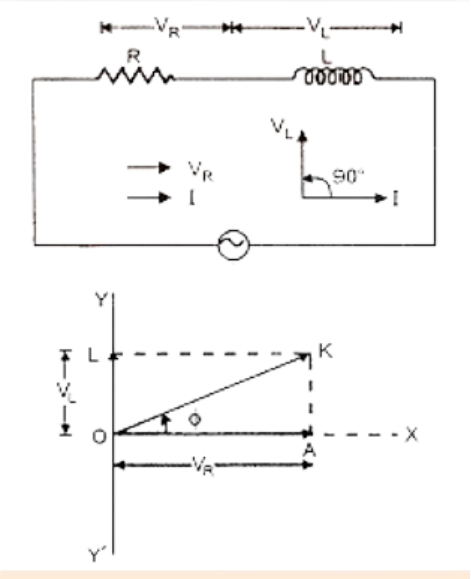
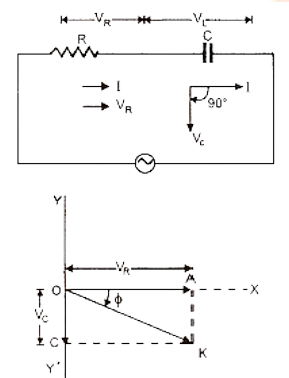
AC voltage in resistors, inductors, capacitors, LCR Circuits
Phasors, Diagram and Analytical Solution
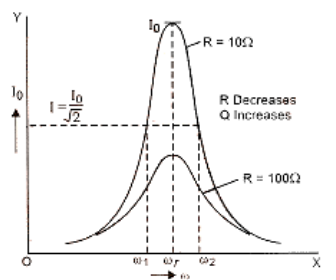
Resonance
The Power Factor
LC Oscillations
Transformers.
6. What are the important formulae in Class 12, Chapter 7 of Physics?
The list of some of the most important formulae in Chapter 7 are stated below:
Alternating current: I=Imsinωt
Alternating voltage: V = Vm sinωt
RMS Value of AC, Irms=I0/ √2
RMS Value of Voltage: Vrms=2V0/ √2
Mean value of AC: Iav=2I0/ π
Power: Pav= Vrms. Irms. Cos φ
7. What is an alternating current in Class 12 Physics Chapter 7?
Chapter 7 of Class 12 Chemistry is titled ‘Alternating Current’. This term is defined as current in which both magnitude and direction vary periodically. Alternating current is defined as a current that changes its magnitude and polarity continuously at a particular point in time. This means that its interval is always fixed. This difficult concept, along with others in the chapter, is explained in precise terms in revision notes specially designed for the exam preparation of students.
8. What is the importance of AC circuits in Class 12 Physics Chapter 7 Alternating Current?
AC circuits are a key concept in Chapter 7, helping students understand how alternating current works in various electrical systems.
9. How does a transformer work in Class 12 Physics Chapter 7?
A transformer changes the voltage levels in AC circuits through electromagnetic induction, making it an essential device discussed in this chapter.
10. What is resonance in AC circuits as explained in Class 12 Physics Chapter 7?
Resonance occurs when the inductive reactance and capacitive reactance are equal, leading to maximum current flow in the circuit.