Maths Notes for Chapter 4 Parts and Wholes Class 5 - FREE PDF Download
FAQs on Parts and Wholes Class 5 Maths Chapter 4 CBSE Notes - 2025-26
1. Is it necessary to download NCERT Class 5 Maths Parts and Wholes solutions?
NCERT Solutions Class 5 Maths Chapter 4 will be necessary to find out how to solve the questions aptly. Practicing using the solutions given will give you better approaches to accurately solving these exercise questions.
2. How can I learn and evaluate my skills in solving fraction problems of Maths Chapter 4 Parts and Wholes Class 5 Notes?
Focus on how our experts have solved the worksheet problems. Identify the patterns of these questions and practice. You will be able to resolve your doubts using the revision notes. This is how you can gather knowledge and sharpen your problem-solving skills.
3. How are wholes different from parts in Class 5 Maths Chapter 4?
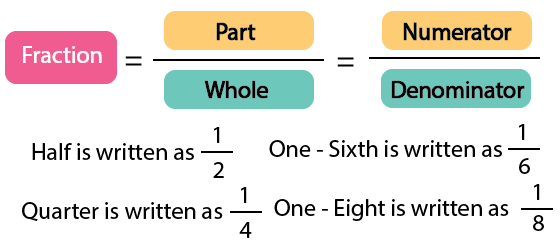
A whole is considered when an entire area is represented or used. A part is defined as the fraction of an area used to represent something.
4. Can I rely solely on these notes for my Class 5 Maths exam preparation?
While these notes are helpful study aids, it's advisable to complement them with the official textbooks, classroom notes, and additional study materials to ensure a thorough understanding of the subject.
5. Do these notes include practice exercises and examples for better understanding of class 5 maths chapter 4 notes PDF?
Many Class 5 Maths notes, including those on "Parts and Wholes," incorporate practice exercises and examples to reinforce learning.
6. How can I ensure the quality and accuracy of the Class 5 Maths Chapter 4 notes on Parts and Wholes I download?
It's advisable to use Vedantu. Additionally, cross-referencing the notes with your official textbooks and consulting with teachers can help verify their accuracy.
7. What is Chapter 4: Parts and Wholes about in Class 5 Maths?
Chapter 4 teaches you about fractions, dividing things into parts, and understanding how parts make up a whole.
8. What are equivalent fractions in Chapter 4 of Class 5 Maths?
Equivalent fractions are different fractions that represent the same amount. For example, $\frac{1}{2}$ is the same as $\frac{2}{4}$.
9. What is the best way to simplify fractions in Class 5 Maths Chapter 4?
Divide both the numerator and the denominator by their greatest common divisor (GCD) to simplify fractions.
10. Why are fractions important in Class 5 Maths Chapter 4?
Fractions help you understand and work with parts of a whole, which is useful in everyday life and for solving more complex maths problems.
11. How can I understand fractions better in Class 5 Maths Chapter 4?
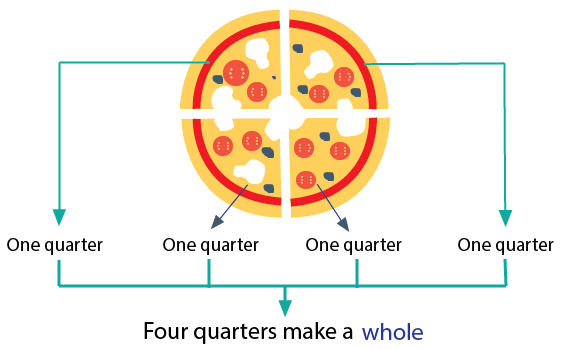
Use everyday objects like pizza slices or fruits to visualise fractions. This helps you see how parts fit into a whole.